
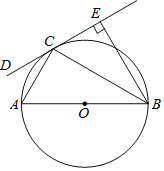
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC,BC.
(1)求证:BC平分∠ABE;
(2)若⊙O的半径为3,cosA=![]() ,求CE的长.
,求CE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据切线的性质得OC⊥DE,则可判断OC∥BE,根据平行线的性质得∠OCB=∠CBE,加上∠OCB=∠CBO,所以∠OBC=∠CBE;
(2)由已知数据可求出AC,BC的长,易证△BEC∽△BCA,由相似三角形的性质即可求出CE的长.
(1)证明:∵CD是⊙O的切线,
∴OC⊥DE,
而BE⊥DE,
∴OC∥BE,
∴∠OCB=∠CBE,
而OB=OC,
∴∠OCB=∠CBO,
∴∠OBC=∠CBE,
即BC平分∠ABE;
(2)∵⊙O的半径为3,
∴AB=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵cosA=![]() ,
,
∴![]() =
=![]() ,
,
∴AC=2![]() ,
,
∴BC=![]() =2
=2![]() ,
,
∵∠ABC=∠ECB,∠ACB=∠BEC=90°,
∴△BEC∽△BCA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某体育用品商店购进一批乒乓球拍,每件进价为10元,售价为30元,每星期可卖出40件.商家决定降价促销,根据市场调查,每降价1元,每星期可多卖出4件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
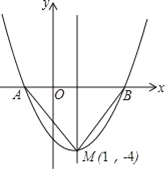
【题目】如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4)
(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=![]() S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移3个单位,再向上平移3个单位得到抛物线
先向右平移3个单位,再向上平移3个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
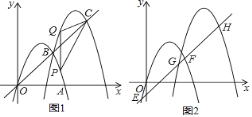
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() 间的一点,作
间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,使
为何值时,使![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
(3)如图2,将直线![]() 向下平移,交抛物线
向下平移,交抛物线![]() 于点
于点![]() ,
,![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,
,![]() ,则
,则![]() 的值是否为定值,证明你的结论.
的值是否为定值,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
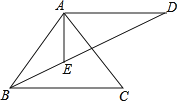
【题目】如图,AE、BE是△ABC的两个内角的平分线,过点A作AD⊥AE.交BE的延长线于点D.若AD=AB,BE:ED=1:2,则cos∠ABC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC
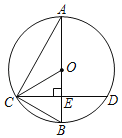
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的一半
B.任意给定一个正方形,一定存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍
C.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半
D.任意给定一个矩形,一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
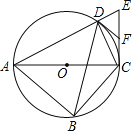
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色植物销售公司打算销售某品种的“赏叶植物”,在针对这种“赏叶植物”进行市场调查后,绘制了以下两张函数图象.其中图①为一条直线,图②为一条抛物线,且抛物线顶点为(6,1),请根据图象解答下列问题:
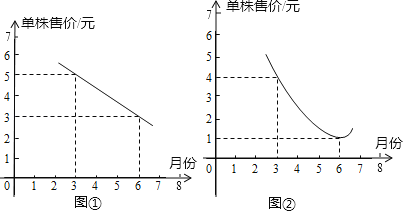
(1)如果公司在3月份销售这种“赏叶植物”,单株获利多少元;
(2)请直接写出图象①中直线的解析式;
(3)请你求出公司在哪个月销售这种“赏叶植物”,单株获利最大?(备注:单株获利=单株售价﹣单株成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com