
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
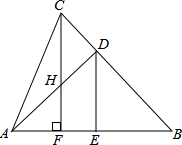 如图,已知在△ABC中,BA=BC,∠B=45°,将△ABC折叠,使点B与点A重合,折痕为DE,CF⊥AB于F,交AD于H,求证:△AFH≌△CDH.
如图,已知在△ABC中,BA=BC,∠B=45°,将△ABC折叠,使点B与点A重合,折痕为DE,CF⊥AB于F,交AD于H,求证:△AFH≌△CDH.查看答案和解析>>
科目:初中数学 来源: 题型:
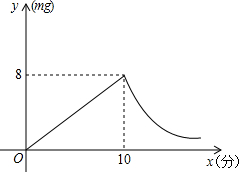 为预防“手足口病”,某校对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量为y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:
为预防“手足口病”,某校对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量为y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com