
【题目】如图所示,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;②
;②![]() 一定是等腰三角形;③
一定是等腰三角形;③![]() ;④
;④![]() ,
,
其中正确结论的序号是________.

【答案】①③④
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,对边相等可得PF=EC,再判断出△PDF是等腰直角三角形,然后根据等腰直角三角形的斜边等于直角边的![]() 倍解答即可.
倍解答即可.
如图,连接PC,
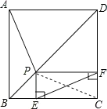
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,

∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,
∴△PDF是等腰直角三角形,
∴PD=![]() PF,
PF,
又∵矩形的对边PF=EC,
∴PD=![]() EC,故④正确;
EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成任务。
筝形的定义:两组邻边分别相等的四边形叫做筝形,几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说,如图,若四边形ABCD是一个筝形,则AB=AD,BC=CD;若AB=AD,BC=CD,则四边形ABCD是筝形.
如图,四边形ABCD是一个筝形,其中AB=AD,BC=CD.对角线AC,BD相交于点O,过点0作0M⊥AB,ON⊥AD,垂足分别为M,N.求证:四边形AMON是筝形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图![]() 分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间
分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间![]() (分钟)之间的函数关系,则以下判断错误的是 ( )
(分钟)之间的函数关系,则以下判断错误的是 ( )

A.骑车的同学比步行的同学晚出发30分钟
B.骑车的同学比步行的同学早6分钟到达目的地
C.骑车的同学从出发到追上步行的同学用了20分钟
D.步行同学的速度是6千米/小时,骑车同学的速度是![]() 千米/小时.
千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,ΔDCE都是等边三角形,且B,C,E在同一条直线上,连接BD与AC交于点M,连接AE与CD交于点N,BD与AE交于点O.给出下列五个结论:①CD∥AB;②BD=AE;③CM=CN;④AO=OE;⑤∠AOD=120°.则其中正确结论有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com