
 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
分析 连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2017=336×6+1,因此点B1向右平移1344(即336×4)即可到达点B2017,根据点B5的坐标就可求出点B2017的坐标.
解答 解:连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.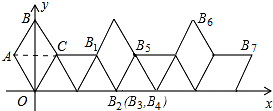
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2017=336×6+1,
∴点B1向右平移1344(即336×4)到点B2017.
∵B1的坐标为(1.5,$\frac{\sqrt{3}}{2}$),
∴B2017的坐标为(1.5+1344,$\frac{\sqrt{3}}{2}$),
∴B2017的坐标为(1345.5,$\frac{\sqrt{3}}{2}$).
故选D.
点评 本题考查了菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
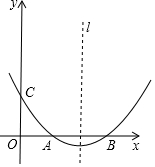 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
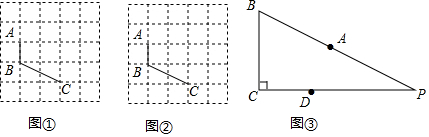
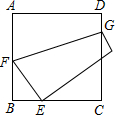 如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$.
如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com