练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．用一条长为40cm的绳子围成一个面积为75cm2的矩形，问矩形的长和宽各是多少？

    分析 设矩形的长为xcm，则矩形的宽为（20-x）cm，根据长＞宽可得出x的取值范围，再根据矩形的面积为75cm2，即可得出关于x的一元二次方程，解方程即可得出x的值，结合x的取值范围即可得出矩形的长和宽．

    解答 解：设矩形的长为xcm，则矩形的宽为（20-x）cm，
    ∵x＞20-x，
    ∴x＞10．
    ∵矩形的面积为75cm2，
    ∴x•（20-x）=75，整理得：x2-20x+75=0，
    解得：x1=5（舍去），x2=15．
    ∴20-x=5．
    答：矩形的长为15cm，宽为5cm．

    点评 本题考查了一元二次方程的应用，根据数量关系列出关于x的一元二次方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图，AB=DC，∠A=∠D，求证：∠ABC=∠DCB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．9m-{159-[4m-（11n-2m）-10n]+2m}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

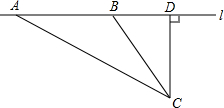    15．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于30m，在l上点D的同侧取点A，B，使∠CAD=30°，∠CBD=60°．．
    （1）求BD的长；
    （2）求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

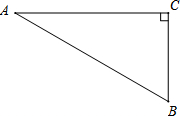    2．已知：如图，在△ABC中，∠C=90°，∠A=30°．
    （1）用直尺和圆规作AB的垂直平分线，分别交AC、AB于点E、D（保留作图痕迹，不写作法）．
    （2）猜想AC与CE之间的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

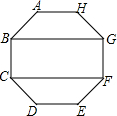    12．如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm2．
    （1）求∠A的度数．
    （2）若点A到线段BG的距离是a，求a2．
    （3）求正八边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知关于x的一元二次方程x2+mx+m-1=0有两个相等的实数根．求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在平面直角坐标系中，如果某点P的横坐标和纵坐标相等，则称点P为“梦之点”．例如点（1，1），（-2016，-2016），（-$\sqrt{3}$，-$\sqrt{3}$），…，都是“梦之点”．
    （1）分别判断函数y=-2x+1和y=x2+1的图象上是否存在“梦之点”？若存在，求出点“梦之点”的坐标；
    （2）若二次函数y=ax2+4x+c的图象上有且只有一个“梦之点”（$\frac{3}{2}$，$\frac{3}{2}$），且当0≤x≤m时，函数y=ax2+4x+c-$\frac{3}{4}$（a≠0）的最小值为-3，最大值为1，求m的取值范围；
    （3）直线l：y=kx+2经过“梦之点”P，与x轴交于点D，与反比例函数y=$\frac{n}{x}$的图象交于M，N两点（点M在点N的左侧），若点P的横坐标为1，且满足DM+DN＜3$\sqrt{2}$，请直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\frac{2}{\sqrt{48}}$；
    （2）$\frac{\sqrt{2{x}^{3}}}{\sqrt{8x}}$；
    （3）$\sqrt{\frac{3}{2}}$÷$\sqrt{\frac{1}{8}}$；
    （4）$\sqrt{\frac{9x}{64{y}^{2}}}$．

    查看答案和解析>>

    同步练习册答案