
����Ŀ����������ͼ�������ʡ���չѧϰƬ��չʾ��
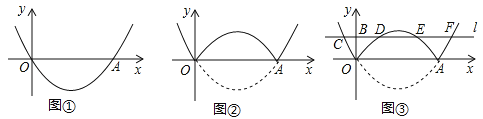
�����⡿��ͼ������ƽ��ֱ������ϵ�У�������y=a��x��2��2��![]() ����ԭ��O����x�����һ������ΪA����a= ��
����ԭ��O����x�����һ������ΪA����a= ��
����������ͼ������������x���·��IJ�����x���۵���x���Ϸ������ⲿ��ͼ����ԭ������ʣ�ಿ�ֵ�ͼ����ɵ���ͼ���ΪG����ͼ����ֱ��д��ͼ��G��Ӧ�ĺ�������ʽ��
��̽������ͼ���У�����B��0��1����ֱ��lƽ����x�ᣬ��ͼ��G�Ľ��������������Ϊ��C��D��E��F����ͼ������ͼ��G��ֱ��l�Ϸ��IJ��ֶ�Ӧ�ĺ���y��x���������ʱx��ȡֵ��Χ��
��Ӧ�á�P��ͼ����ͼ��G��һ�㣬�������Ϊm������PD��PE��ֱ��д����PDE�������С��1ʱm��ȡֵ��Χ��
���𰸡������⡿��a=![]() ������������y=
������������y= ����̽��������1��x��2��x��2+
����̽��������1��x��2��x��2+![]() ʱ������y��x���������Ӧ�á���m=0��m=4��m��2��
ʱ������y��x���������Ӧ�á���m=0��m=4��m��2��![]() ��m��2+
��m��2+![]() ��
��
��������
��������������⡿���ѣ�0��0����������a��ֵ��
������������д����x���۵������������ߵĽ���ʽ������ͼ��ɵö�Ӧȡֵ�Ľ���ʽ��
��̽��������y=0���ֱ�������������ߵĽ���ʽ���ֱ�����ĸ���CDEF�����꣬����ͼ����������ƵIJ��֣���y��x���������д��x��ȡֵ��
��Ӧ�á�������DE�ij������������������ߵ�ȡֵh��1��
�������ֽ������ۣ�
����P��C������F���Ҳಿ��ʱ����P[m��![]() ]������h��1���в���ʽ������ɣ�
]������h��1���в���ʽ������ɣ�
����ͼ�������Գ�����������С��1��֪����P��������DE���Ϸ���
��P��O��A�غ�ʱ������������m=0��m=4��
��������������⡿
��������y=a��x��2��2��![]() ����ԭ��O��
����ԭ��O��
��0=a��0��2��2��![]() ��
��
a=![]() ��
��
������������ͼ���������ߣ�y=![]() ��x��2��2��
��x��2��2��![]() ��
��
�Գ����ǣ�ֱ��x=2���ɶԳ��Եã�A��4��0����
��x���۵�������������Ϊ��y=��![]() ��x��2��2+
��x��2��2+![]()
��ͼ����ͼ��G��Ӧ�ĺ�������ʽΪ��y= ��
��
��̽��������ͼ����������ã�
��y=1ʱ��![]() ��x��2��2��
��x��2��2��![]() =0��
=0��
��ã�x1=2+![]() ��x2=2��
��x2=2��![]() ��
��
��C��2��![]() ��1����F��2+
��1����F��2+![]() ��1����
��1����
��y=1ʱ����![]() ��x��2��2+
��x��2��2+![]() =0��
=0��
��ã�x1=3��x2=1��
��D��1��1����E��3��1����
��ͼ��ã�ͼ��G��ֱ��l�Ϸ��IJ��֣���1��x��2��x��2+![]() ʱ������y��x���������
ʱ������y��x���������
��Ӧ�á�����D��1��1����E��3��1����
��DE=3��1=2��
��S��PDE= ![]() DEh��1��
DEh��1��
��h��1��
����P��C������F���Ҳಿ��ʱ����P[m��![]() ]��
]��
��h=![]() ��m��2��2��
��m��2��2��![]() ��1��1��
��1��1��
��m��2��2��10��
m��2��![]() ��m��2����
��m��2����![]() ��
��
m��2+![]() ��m��2��
��m��2��![]() ��
��
����ͼ�������Գ��ύ������G��H����ֱ��CD��M����x����N��
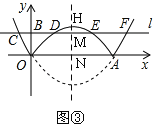
��H��2��![]() ����
����
��HM=![]() ��1=
��1=![]() ��1��
��1��
������P��������DE���Ϸ���
�ۡ�MN=1��
��O��0��0����a��4��0����
��P��O��A�غ�ʱ������������
��m=0��m=4��
������������PDE�������С��1ʱ��m��ȡֵ��Χ�ǣ�m=0��m=4��m��2��![]() ��m��2+
��m��2+![]() ��
��


 �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
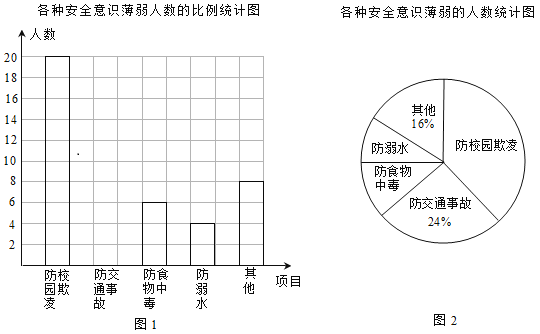
����Ŀ��ijУ��֯��һ�η���ˮ������ͨ�¹ʡ���ʳ���ж�����У���輰�������ְ�ȫ��ʶ�ĵ������˽�ͬѧ������Щ����İ�ȫ��ʶ���������ڽ����õؿ�չ��ȫ����������ݵ����������Ƴ�ͼ1��ͼ2������������ͳ��ͼ��
����ͼ�е���Ϣ����������⣺
(1)���ε��������Ϊ___________�����з�У������ʶ����������ռ_________%��
(2)��ȫ����ͳ��ͼ��
(3)����У����1500��ѧ��������Ƹ�Уѧ���з���ˮ��ʶ������������
(4)����������е���Ϣ������У�İ�ȫ������һ�������Ľ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��L1��y=k1x+b1 �� L2��y=k2x+b2 �� ��L1��L2 �� ����k1k2=��1��
��1��Ӧ�ã���֪y=2x+1��y=kx��1��ֱ����k��
��2��ֱ�߾���A��2��3��������y= ![]() x+3��ֱ�������ʽ��
x+3��ֱ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ѧ��ѵ���ѵ���У�С��ͬѧ������ɼ�����λ������Ϊ��5��7��9��10��7�����������ݵ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB�뺯��y��![]() ��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��
��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��![]() OC������ACD�������6������BC��
OC������ACD�������6������BC��
��1����m��k��n��ֵ��
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��PA��һ�κ���y=x+1��ͼ��ֱ��PB��һ�κ���y=��2x+2��ͼ��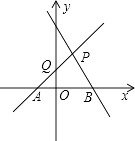
��1����A��B��P��������ꣻ
��2�����ı���PQOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
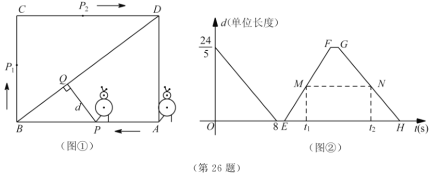
����Ŀ��ijУ��������ȤС������ͼ����ʾ�ľ��γ����Ͽ�չѵ���������˴ӵ�![]() �������ھ���
�������ھ���![]() ��������
��������![]() �ķ��������ƶ��������
�ķ��������ƶ��������![]() ʱֹͣ�ƶ�����֪�����˵��ٶ�Ϊ
ʱֹͣ�ƶ�����֪�����˵��ٶ�Ϊ![]() ����λ����/
����λ����/![]() ���ƶ����սǴ�����������Ҫ
���ƶ����սǴ�����������Ҫ![]()
![]() ������
������![]() ��
��![]() ������ʱ�ֱ���ʱ
������ʱ�ֱ���ʱ![]()
![]() ���������������ʱ��Ϊ
���������������ʱ��Ϊ![]() ʱ��������λ���õ�
ʱ��������λ���õ�![]() ��ʾ��
��ʾ��![]() ���Խ���
���Խ���![]() �ľ��루�����߶�
�ľ��루�����߶�![]() �ij���Ϊ
�ij���Ϊ![]() ����λ���ȣ�����
����λ���ȣ�����![]() ��
��![]() �ĺ���ͼ����ͼ����ʾ��
�ĺ���ͼ����ͼ����ʾ��
��1����![]() ��
��![]() �ij���
�ij���
��2����ͼ������![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϣ��߶�
�ϣ��߶�![]() ƽ���ں��ᣬ
ƽ���ں��ᣬ![]() ��
��![]() �ĺ�����ֱ�Ϊ
�ĺ�����ֱ�Ϊ![]() ��
��![]() �������������
�������������![]() �����
�����![]() ��������
��������![]() �����
�����![]() ������ͼ��������
������ͼ��������![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
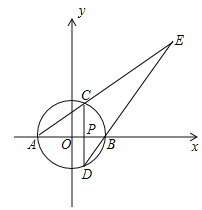
����Ŀ����ͼ����ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ��x��ֱ���A��B���㣨��B�ڵ�A���ұߣ���P�ǰ뾶OB��һ�㣬��P�Ҵ�ֱ��AB��ֱ������O�ֱ���C��D���㣨��C�ڵ�D���Ϸ�����ֱ��AC��DB���ڵ�E����AC��CE=1��2��
��1�����P�����ꣻ
��2�������A�͵�E���Ҷ�����ֱ��CD�ϵ������ߵĺ�������ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com