
【题目】如图,已知抛物线y=﹣x2+bx+3的对称轴为直线x=﹣1,分别与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)求b的值;
(2)若将线段BC绕点C顺时针旋转90°得到线段CD,问:点D在该抛物线上吗?请说明理由.
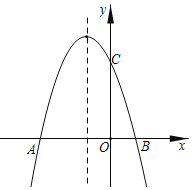
【答案】(1)b=﹣2;(2)点D不在该抛物线上,见解析
【解析】
(1)根据抛物线的对称轴公式,可求出b的值,
(2)确定函数关系式,进而求出与x轴、y轴的交点坐标,由旋转可得全等三角形,进而求出点D的坐标,代入关系式验证即可.
解:(1)∵抛物线y=﹣x2+bx+3的对称轴为直线x=﹣1,
∴![]() =﹣1,
=﹣1,
∴b=﹣2;
(2)当x=0时,y=3,因此点C(0,3),即OC=3,
当y=0时,即﹣x2+bx+3=0,解得x1=﹣3,x2=1,因此OB=1,OA=3,
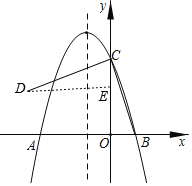
如图,过点D作DE⊥y轴,垂足为E,由旋转得,CB=CD,∠BCD=90°,
∵∠OBC+∠BCO=90°=∠BCO+∠ECD,
∴∠OBC=∠ECD,
∴△BOC≌△CDE (AAS),
∴OB=CE=1,OC=DE=3,
∴D(﹣3,2)
当x=﹣3时,y=﹣9+6+3=0≠2,
∴点D不在该抛物线上.


科目:初中数学 来源: 题型:
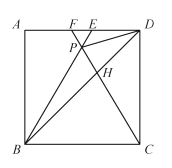
【题目】如图,在正方形![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() 的延长线分别交
的延长线分别交![]() 于点
于点![]() ,连结
,连结![]() 与
与![]() 相交于点H.给出下列结论,
相交于点H.给出下列结论,
①△ABE≌△DCF;②△DPH是等腰三角形;③![]() ;④
;④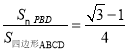 ,
,
其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
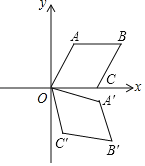
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家![]() 他60岁时完成的
他60岁时完成的![]() 直指算法统宗
直指算法统宗![]() 是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法
是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法![]() 对书中某一问题改编如下:
对书中某一问题改编如下:
一百馒头一百僧,大僧三个更无争;
小僧三人分一个,大僧共得几馒头.
一百馒头一百僧,大僧三个更无争;
小僧三人分一个,大僧共得几馒头.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个正好分完,大和尚共分得![]()
![]() 个馒头
个馒头
A. 25B. 72C. 75D. 90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象经过点
)的图象经过点![]() 和
和![]() ,直线
,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
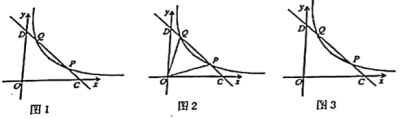
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 、
、![]() ,当
,当![]() 时,求此时
时,求此时![]() 的值:
的值:
(3)如图3,点![]() ,点
,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴正半轴上的动点.再以
轴正半轴上的动点.再以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .若点
.若点![]() 恰好在函数
恰好在函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象上,且四边形
)的图象上,且四边形![]() 为平行四边形,求此时
为平行四边形,求此时![]() 、
、![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).
(1)画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.

查看答案和解析>>
科目:初中数学 来源: 题型:
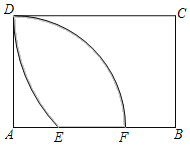
【题目】如图,以矩形ABCD的顶点A为圆心,线段AD长为半径画弧,交AB边于F点;再以顶点C为圆心,线段CD长为半径画弧,交AB边于点E,若AD=![]() ,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
,CD=2,则DE、DF和EF围成的阴影部分面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com