
【题目】如图,已知□ABCD中,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,求证:AE⊥DE.

【答案】见解析
【解析】试题分析:(1)根据DE是∠ADC的角平分线,得到∠ADE=∠CDE,再根据平行四边形的性质得到∠ADE=∠DEC.所以∠CDE=∠DEC,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到AB=BE, ∠BAE=∠BEA.
推出∠DAE=∠BAE=![]() ∠BAD.再根据平行四边形邻角互补得到∠BAD+∠ADC=180°,
∠BAD.再根据平行四边形邻角互补得到∠BAD+∠ADC=180°,
∠DAE+∠ADE=![]() (∠BAD+∠ADC)=90°,从而证明AE⊥DE.
(∠BAD+∠ADC)=90°,从而证明AE⊥DE.
试题解析:(1)∵ 四边形ABCD是平行四边形,
∴ AD∥BC,
∴ ∠ADE=∠DEC.
∵ DE是∠ADC的角平分线,
∴ ∠ADE=∠CDE,
∴ ∠CDE=∠DEC,
∴ CD=CE.
(2)∵ 四边形ABCD是平行四边形,
∴ AB=DC.
∵ CD=CE,BE=CE
∴ AB=BE,
∴ ∠BAE=∠BEA.
∵ AD∥BC,
∴ ∠DAE=∠BEA.
∴ ∠DAE=∠BAE=![]() ∠BAD.
∠BAD.
∵ AB∥DC,
∴ ∠BAD+∠ADC=180°,
∵ ∠ADE=![]() ∠ADC,
∠ADC,
∴ ∠DAE+∠ADE=![]() (∠BAD+∠ADC)=90°,
(∠BAD+∠ADC)=90°,
∴ ∠AED=90°,
∴ AE⊥DE.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,∠DBM=∠DAN,DM⊥BE于M,DN⊥AC于N.(1)求证:△BDM≌△ADN ;(2)若AC=2,BC=1,求CM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“有理数的加法与减法运算”的学习过程中,我们做过如下数学实验.“把笔尖放在数轴的原点处,先向左移动3个单位长度,再向右移动1个单位长度,这时笔尖的位置表示什么数?”用算式表示以上过程和结果的是( )
A. (﹣3)﹣(+1)=﹣4 B. (﹣3)+(+1)=﹣2 C. (+3)+(﹣1)=+2 D. (+3)+(+1)=+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
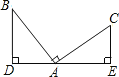
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A,B两点对应的数分别为a,b,且a,b满足|a+20|=﹣(b﹣13)2,点C对应的数为16,点D对应的数为﹣13.
(1)求a,b的值;
(2)点A,B沿数轴同时出发相向匀速运动,点A的速度为6个单位/秒,点B的速度为2个单位/秒,若t秒时点A到原点的距离和点B到原点的距离相等,求t的值;
(3)在(2)的条件下,点A,B从起始位置同时出发.当A点运动到点C时,迅速以原来的速度返回,到达出发点后,又折返向点C运动.B点运动至D点后停止运动,当B停止运动时点A也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE![]() AB;(2)AE=BE.
AB;(2)AE=BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com