
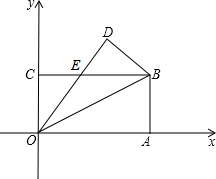
 如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.分析 (1)由折叠得到∠DOB=∠AOB,再由BC∥OA得到∠OBC=∠AOB,即∠OBC=∠DOB,即可;
(2)由(1)得到EO=EB设OE=x则DE=8-x,再用勾股定理建立方程16+(8-x)2=x2,求出x即可;
(3)设出点P坐标,分三种情况讨论计算即可;
(4)根据题意判断出过点D作OA的垂线交OB于M,OA于N,求出DM即可.
解答 解:(1)∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB,
(2)由(1)有,EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=x,则DE=8-x,
在Rt△BDE中,BD=4,根据勾股定理得,DB2+DE2=BE2,
∴16+(8-x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴E(3,4),
(3)点B的坐标为(8,4),
∴直线OB解析式为y=$\frac{1}{2}$x,
∵点P是直线OB上的任意一点,
∴设P(a,$\frac{1}{2}$a),
∵O(0,0),C(0,4),
∴OC=4,PO2=a2+($\frac{1}{2}$a)2=$\frac{5}{4}$a2,PC2=a2+(4-$\frac{1}{2}$a)2,
∵△OPC是等腰三角形
①当PO=PC时,∴PO2=PC2,
∴$\frac{5}{4}$a2=a2+(4-$\frac{1}{2}$a)2,
∴a=4,
∴P(4,2),
②当PO=OC时,∴PO2=OC2,
∴$\frac{5}{4}$a2=16,
∴a=±$\frac{8\sqrt{5}}{5}$,
∴P($\frac{8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$)或P(-$\frac{8\sqrt{5}}{5}$,-$\frac{4\sqrt{5}}{5}$),
③当PC=OC时,∴PC2=OC2,
∴a2+(4-$\frac{1}{2}$a)2=16,
∴a=0(舍)或a=$\frac{16}{5}$,
∴P($\frac{16}{5}$,$\frac{8}{5}$);
∴满足条件的点P的坐标为(4,2)或($\frac{16}{5}$,$\frac{8}{5}$)或($\frac{8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$)或(-$\frac{8\sqrt{5}}{5}$,-$\frac{4\sqrt{5}}{5}$),
(4)如图,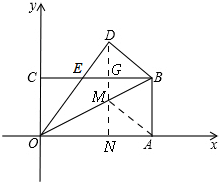
过点D作OA的垂线交OB于M,交OA于N,此时的M,N是AM+MN的最小值的位置,求出DN就是AM+MN的最小值,
由(2)有,DE=3,BE=5,BD=4,
∴根据面积有DE×BD=BE×DG,
∴DG=$\frac{DE×BD}{BE}$=$\frac{12}{5}$,
由题意有,GN=OC=4,
∴DN=DG+GN=$\frac{12}{5}$+4=$\frac{32}{5}$.
即:AM+MN的最小值为$\frac{32}{5}$.
点评 此题是几何变换综合题,主要考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的性质,极值的确定,解本题的关键求出点E的坐标.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).
在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m与4的差是负数,可表示为m-4<0 | B. | x不大于3可表示为x<3 | ||
| C. | a是负数可表示为a>0 | D. | x与2的和是非负数可表示为x+2>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | -7 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com