
【题目】如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
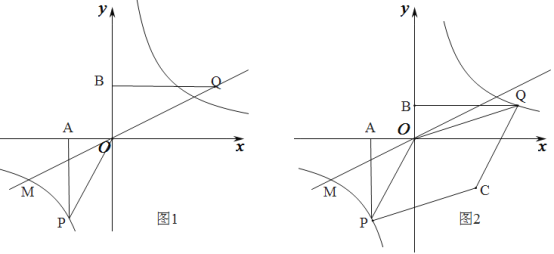
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
【答案】(1)y=![]() x,
x,![]() ;(2)存在,Q1(2,1)和Q2(﹣2,﹣1);(3)2
;(2)存在,Q1(2,1)和Q2(﹣2,﹣1);(3)2![]() +4
+4
【解析】
(1)正比例函数和反比例函数的图象都经过点M(-2,-1),待定系数法可求它们解析式;
(2)由点Q在y=![]() x上,设出Q点坐标,表示△OBQ,由反比例函数图象性质,可知△OAP面积为1,则根据面积相等可构造方程,问题可解;
x上,设出Q点坐标,表示△OBQ,由反比例函数图象性质,可知△OAP面积为1,则根据面积相等可构造方程,问题可解;
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,而点P(-1,-2)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
解:(1)设正比例函数解析式为y=kx,
将点M(﹣2,﹣1)坐标代入得k=![]() ,所以正比例函数解析式为y=
,所以正比例函数解析式为y=![]() x,
x,
同样可得,反比例函数解析式为![]() ;
;
(2)当点Q在直线OM上运动时,
设点Q的坐标为Q(m,![]() m),
m),
于是S△OBQ=![]() OBBQ=
OBBQ=![]() ×
×![]() m×m=
m×m=![]() m2,
m2,
而S△OAP=|![]() (﹣1)×(﹣2)|=1,
(﹣1)×(﹣2)|=1,
所以有,![]() m2=1,解得m=±2,
m2=1,解得m=±2,
所以点Q的坐标为Q1(2,1)和Q2(﹣2,﹣1);
(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,
而点P(﹣1,﹣2)是定点,所以OP的长也是定长,
所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,
因为点Q在第一象限中双曲线上,所以可设点Q的坐标为Q(n,![]() ),
),
由勾股定理可得OQ2=n2+![]() =(n﹣
=(n﹣![]() )2+4,
)2+4,
所以当(n﹣![]() )2=0即n﹣
)2=0即n﹣![]() =0时,OQ2有最小值4,
=0时,OQ2有最小值4,
又因为OQ为正值,所以OQ与OQ2同时取得最小值,
所以OQ有最小值2,由勾股定理得OP=![]() ,
,
所以平行四边形OPCQ周长的最小值是2(OP+OQ)=2(![]() +2)=2
+2)=2![]() +4.
+4.
(或因为反比例函数是关于y=x对称,所以当Q在反比例函数时候,OQ最短的时候,就是反比例与y=x的交点时候,联立方程组即可得到点Q坐标)


科目:初中数学 来源: 题型:
【题目】某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似地看作一次函数
(元)之间的关系可近似地看作一次函数![]() .物价部门规定该品牌的护眼灯售价不能超过36元.
.物价部门规定该品牌的护眼灯售价不能超过36元.
(1)如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?
(2)设该商店每月获得利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
(元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
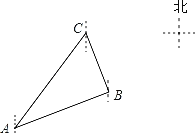
【题目】在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 个直角边长为3的等腰直角三角形
个直角边长为3的等腰直角三角形![]() ,
,![]() ……,斜边在同一直线上,设
……,斜边在同一直线上,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() …,
…,![]() 的面积为
的面积为![]() ,则
,则![]() _________________;
_________________;![]() _____________.
_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是直线l外一个定点,点A为直线l上一个定点,点P关于直线l的对称点记为P1,将直线l绕点A顺时针旋转30°得到直线l′,此时点P2与点P关于直线l′对称,则∠P1AP2等于( )
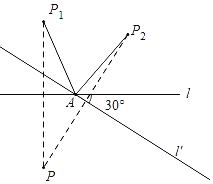
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com