
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
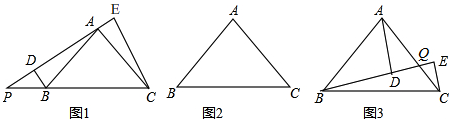
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | |
| B. | 3.142 345 678 | |
| C. | $\frac{3}{11}$ | |
| D. | 0.202 002 000 2…(相邻两个2之间0的个数逐次增加1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
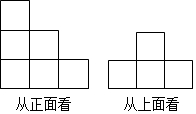 用小立方块搭成的几何体,从正面看和从上面看得到的视图如图,问这样的几何体有多少可能?它最多需要多少小立方块,最少需要多少小立方块,请画出最少和最多时从左面看到的视图.
用小立方块搭成的几何体,从正面看和从上面看得到的视图如图,问这样的几何体有多少可能?它最多需要多少小立方块,最少需要多少小立方块,请画出最少和最多时从左面看到的视图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com