练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1） △AEB ∽ △CBA .

    （或△AEB∽△BFC；△AEB∽△ADC；△CAB∽△BFC；△BFC∽△ADC . ）

    证明：∵四边形ABCD和四边形AEFC是矩形，

    ∴∠E =∠CBA=∠EAC=90°.

    ∵∠EAB+∠CAB=90°，

    ∠EAB+∠ABE=90°，

    ∴∠ABE=∠CAB.

    ∴△AEB ∽ △CBA.

    （2）解：∵△AEB ∽ △CBA，

    ∴ . ∴.

    ∵

    ∴.


    （1） △AEB ∽ △CBA .

    （或△AEB∽△BFC；△AEB∽△ADC；△CAB∽△BFC；△BFC∽△ADC . ）

    证明：∵四边形ABCD和四边形AEFC是矩形，

    ∴∠E =∠CBA=∠EAC=90°.

    ∵∠EAB+∠CAB=90°，

    ∠EAB+∠ABE=90°，

    ∴∠ABE=∠CAB.

    ∴△AEB ∽ △CBA.

    （2）解：∵△AEB ∽ △CBA，

    ∴ . ∴.

    ∵

    ∴.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，四边形是平行四边形，以对角线为直径作⊙，分别于、相交于点、．

    （1）求证四边形为矩形．

    （2）若试判断直线与⊙的位置关系，并说明理由．

    查看答案和解析>>

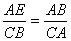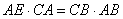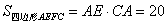    科目：初中数学 来源： 题型：


    如图，以等边三角形ABC的BC边为直径画半圆，分别交AB、AC于点E、D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为       ．

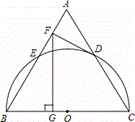
    查看答案和解析>>

    科目：初中数学 来源： 题型：


     在正方形网格中，△ABC的位置如图所示，则sin B的值是

    A.         B．       C．        D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=m，已知木箱高BE=m，斜面坡角为30°，则木箱端点E距地面AC的高度EF为        m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在2014年“元旦”前夕，某商场试销一种成本为30元的文化衫，经试销发现，若每件按34元的价格销售，每天能卖出36件；若每件按39元的价格销售，每天能卖出21件．假定每天销售件数y（件）是销售价格x (元)的一次函数．

      （1）直接写出y与x之间的函数关系式y =                       ．

      （2）在不积压且不考虑其他因素的情况下，每件的销售价格定为多少元时，才能使每天获得的利润P最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有一辆汽车在中途受阻，耽误了6分钟，然后将速度由原来的每小时40千米，提高到每小时50千米，若要将耽误的时间补上，则需这样走(　　)．

    A．10千米                           B．20千米

    C．40千米                           D．50千米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    －＝0.75.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：

    A种产品

    B种产品

    成本(万元/件)

    3

    5

    利润(万元/件)

    1

    2

    (1)若工厂计划获利14万元，问A，B两种产品应分别生产多少件？

    (2)若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？

    (3)在(2)条件下，哪种方案获利最大？并求最大利润．


    查看答案和解析>>

    同步练习册答案