
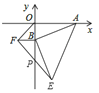
【题目】如图,点A的坐标为(8,0),点B为y轴负半轴上的一动点,分别以OB,AB为直角边在第三、第四象限作等腰直角三角形OBF,等腰直角三角形ABE,连接EF交y轴与P点,当点B在y轴上移动时,则PB的长度是( )
A.2B.4C.不是已知数的定值D.PB的长度随点B的运动而变化
【答案】B
【解析】
作EN⊥y轴于N,求出∠NBE=∠BAO,证△ABO≌△BEN,求出∠OBF=∠FBP=∠BNE=90°,证△BFP≌△NEP,推出BP=NP,即可得出答案.
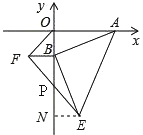
解:如图,作EN⊥y轴于N,
∵∠ENB=∠BOA=∠ABE=90°,
∴∠OBA+∠NBE=90°,∠OBA+∠OAB=90°,
∴∠NBE=∠BAO,
在△ABO和△BEN中,
 ,
,
∴△ABO≌△BEN(AAS),
∴OB=NE=BF,
∵∠OBF=∠FBP=∠BNE=90°,
在△BFP和△NEP中,
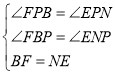 ,
,
∴△BFP≌△NEP(AAS),
∴BP=NP,
又∵点A的坐标为(8,0),
∴OA=BN=8,
∴BP=NP=4,
故选:B.


科目:初中数学 来源: 题型:
【题目】已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
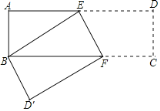
A.6cm2B.8 cm2C.10 cm2D.12 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,动点P从点D出发,沿射线
,动点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段
的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段![]() 上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
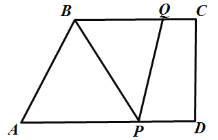
(1)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(2)若四边形![]() 为平行四边形,求运动时间t;
为平行四边形,求运动时间t;
(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字![]() 、
、![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.
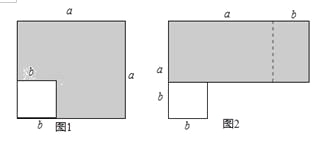
(1)如图1,阴影部分的面积是: ;
(2)如图2,是把图1重新剪拼成的一个长方形,阴影部分的面积是 ;
(3)比较两阴影部分面积,可以得到一个公式是 ;
(4)运用你所得到的公式,计算:99.8×100.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真观察图26.1的4个图中阴影部分构成的图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征.
特征1:_________________________________________________;
特征2:_________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com