
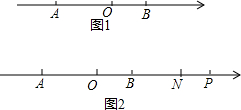
 如图1,点A在数轴上对应的数为-3,点B对应的数为2.
如图1,点A在数轴上对应的数为-3,点B对应的数为2.分析 (1)由数轴上的两点距离公式直接求得;
(2)设出点P代表的数,列式求解即可,要分类讨论;
(3)设P点所表示的数为n,就有PA=n+3,PB=n-2,根据条件就可以表示出PM=$\frac{n+3}{2}$,BN=$\frac{2}{3}$×(n-2),再分别代入PM-$\frac{3}{4}$BN求出其值即可.
解答 解:(1)线段AB的长=2-(-3)=5;
(2)设点P表示的数为x,当点P在点A左侧,根据PA+PB=8,
∴-3-x+2-x=8,解得:x=-4.5,
当点P在点A左侧,根据PA+PB=8,
∴x-(-3)+x-2=8,解得:x=3.5,
当点P在线段AB上时,可求PA+PB=5,与题意不符,
∴点P对应的数为:-4.5和3.5;
(3)设P点所表示的数为n,
∴PA=n+3,PB=n-2.
∵PA的中点为M,
∴PM=$\frac{1}{2}$PA=$\frac{n+3}{2}$.
N为PB的三等分点且靠近于P点,
∴BN=$\frac{2}{3}$PB=$\frac{2}{3}$×(n-2).
∴PM-$\frac{3}{4}$BN=$\frac{n+3}{2}$-$\frac{3}{4}$×$\frac{2}{3}$×(n-2)=$\frac{5}{2}$.
点评 本题主要考查一元一次方程的运用,数轴的运用,数轴上任意两点间的距离公式的运用,对于告诉距离求点时注意分类讨论是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1:1:1 | B. | 1:1:2 | C. | 1:2:2 | D. | 1:2:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
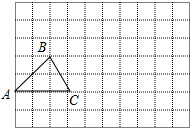 在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.
在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)(4-x) | B. | (-a-3)(3-a) | C. | (a+b)(-a-b) | D. | (2y-4)(-4+2y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com