
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
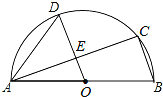
【答案】(1)∠CAD的度数为36°;(2)DE的长为4.
【解析】试题分析:(1)根据圆周角定理可得∠ACB=90°,则∠CAB的度数即可求得,在等腰△AOD中,根据等边对等角求得∠DAO的度数,则∠CAD即可求得;
(2)易证OE是△ABC的中位线,利用中位线定理求得OE的长,则DE即可求得.
试题解析:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,∠CAB=90°-∠B=90°-70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=![]() =55°
=55°
∴∠CAD=∠DAO-∠CAB=55°-20°=35°;
(2)在直角△ABC中,BC=![]() .
.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=![]() BC=
BC=![]() .
.
又∵OD=![]() AB=6.5,
AB=6.5,
∴DE=OD-OE=6.5-![]() =4.
=4.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于F,交AC于E,若EG⊥BC于G,连结FG.说明四边形AFGE是菱形.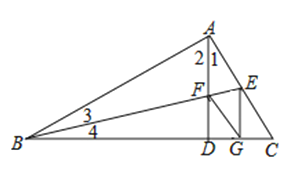
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(mx4)·(4xk)=-12x12,则适合条件的m,k的值分别是( )
A. m=-3,k=8 B. m=3,k=8
C. m=8,k=3 D. m=-3,k=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用直尺画图(先用铅笔画图,然后再用墨水笔将符合条件的图形画出). 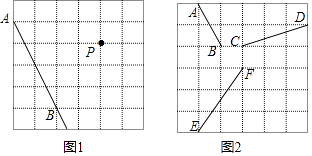
(1)利用图1中的网格,过P点画直线AB的平行线和垂线;
(2)平移图(2)网格中的三条线段AB、CD、EF,使平移后三条线段首尾顺次相接组成一个三角形;
(3)如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com