4．【问题思考】有这么一道数学问题：“若x+2y=5，则代数式5-2x-4y的值为-5”
同学A：我可以选择特殊值法求解，如取x=1，那么y=2，
则所求代数式的值为5-2x-4y=5-2×1-4×2=-5，
同学B：我也可以用整体思想进行求解，设a=x+2y=5，
5-2x-4y=5-2（x+2y）=5-2a=5-2×5=-5
[问题解决】运用上述思想方法解决下列问题：
（1）若代数式a
2+2a的值为5，则代数式5-4a-2a
2的值为-5．
（2）若方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$，则方程组$\left\{\begin{array}{l}{{a}_{1}x+2{b}_{1}y=4{c}_{1}}\\{{a}_{2}x+2{b}_{2}y=4{c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$
（3）方程组$\left\{\begin{array}{l}{2013（x+2）+2014（y+1）=1}\\{2014（x+2）+2013（y+1）=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-3}\\{y=0}\end{array}\right.$
（4）已知分式方程x+$\frac{1}{x}$=2+$\frac{1}{2}$的解为x
1=2，x
2=$\frac{1}{2}$，那么方程x+$\frac{1}{x-1}$=a+$\frac{1}{a-1}$的解为x
1=a，x
2=$\frac{a}{a-1}$．
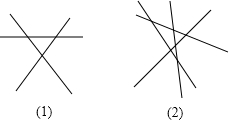
（5）不交于同一点的三条直线两两相交（如图（1））有6对同旁内角；不交于同一点的四条直线两两相交（如图（2）），有24对同旁内角．
【问题迁移】
《怎样解题》的作者波利亚说过：“发现问题、提出问题比分析问题、解决问题更重要，请你提出一个能用整体思想来求解的有关因式分解的问题，并写出解题过程．
如图，是某县交通局欲修一条公路，从A村庄到B村庄，再通往公路MN，以利于村民出行方便，如果你是该局的负责人，应该怎样修才能使所修的公路最短？画出线路图，并说明理由．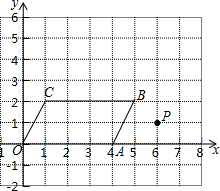
在平面直角坐标系内有一平行四边形点O（0，0），A（4，0），B（5，2），C（1，2），有一次函数y=kx+b的图象过点P（6，1）．
