
【题目】在矩形纸片![]() 中,
中,![]() 是边
是边![]() 上的点,将纸片沿
上的点,将纸片沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为___________.
的长为___________.
【答案】3或6.
【解析】
试题分析:由AD=8、AB=6结合矩形的性质可得出AC=10,△EFC为直角三角形分两种情况:①当∠EFC=90°时,可得出AE平分∠BAC,根据角平分线的性质即可得出![]() ,解之即可得出BE的长度;②当∠FEC=90°时,可得出四边形ABEF为正方形,根据正方形的性质即可得出BE的长度.
,解之即可得出BE的长度;②当∠FEC=90°时,可得出四边形ABEF为正方形,根据正方形的性质即可得出BE的长度.
∵AD=8,AB=6,四边形ABCD为矩形,
∴BC=AD=8,∠B=90°,∴AC=![]() =10.
=10.
△EFC为直角三角形分两种情况:
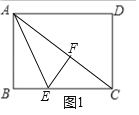
①当∠EFC=90°时,如图1所示.
∵∠AFE=∠B=90°,∠EFC=90°,∴点F在对角线AC上,
∴AE平分∠BAC,∴![]() ,即
,即![]() ,∴BE=3;
,∴BE=3;
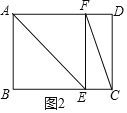
②当∠FEC=90°时,如图2所示.
∵∠FEC=90°,∴∠FEB=90°,∴∠AEF=∠BEA=45°,
∴四边形ABEF为正方形,∴BE=AB=6.
综上所述:BE的长为3或6.
故答案为:3或6.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某篮球队12名队员的年龄如下表所示:
年龄(岁) | 18 | 19 | 20 | 21 |
人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和中位数分别是( )
A.18,19B.18,19.5C.5,4D.5, 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区的电力资源丰富,并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费. 月用电量x(度)与相应电费y(元)之间的函数图像如图所示.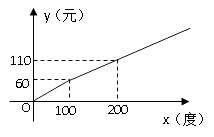
(1)月用电量为100度时,应交电费元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
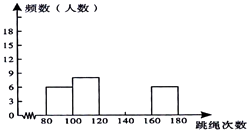
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳
不合格的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.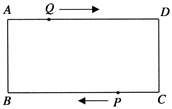
(1)当0<t<3,判断四边形BQDP的形状,并说明理由;
(2)求四边形BQDP的面积S与运动时间t的函数关系式;
(3)求当t为何值时,四边形BQDP为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.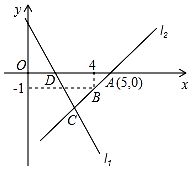
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com