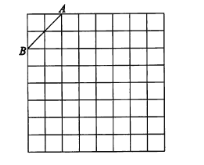
【题目】如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：
(1)在网格中建立平面直角坐标系，使A点坐标为(-2，4)，B点坐标为(-4，2)；
(2)在(1)的前提下，在第二象限内的格点上找一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点的坐标是；
(3)求((2)中△ABC的周长(结果保留根号)；
(4)画出((2)中△ABC关于y轴对称的△A'B'C'.
科目：初中数学 来源： 题型：
【题目】（2016广西桂林市）已知任意三角形的三边长，如何求三角形面积？
古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
（其中a，b，c是三角形的三边长，p=
，S为三角形的面积），并给出了证明
例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：
∵a=3，b=4，c=5，∴p=
=6，∴S=
=
=6．
事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．
如图，在△ABC中，BC=5，AC=6，AB=9
（1）用海伦公式求△ABC的面积；
（2）求△ABC的内切圆半径r．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A、B两名同学在同一个学校上学，B同学上学的路上经过A同学家。A同学步行，B同学骑自行车，某天，A，B两名同学同时从家出发到学校，如图，
A表示A同学离B同学家的路程
A(m)与行走时间
(min)之间的函数关系图象，B表示B同学离家的路程B(m)与行走时间(min)之间的函数关系图象.
（1）A，B两名同学的家相距________m.
（2）B同学走了一段路后，自行车发生故障，进行修理，修理自行车所用的时间是 _____min.
（3）B同学出发后______min与A同学相遇.
（4）求出A同学离B同学家的路程A与时间的函数关系式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整，原题：如图1，在平行四边形ABCD中，点E是BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G.若
＝3，求
的值．
(1)尝试探究：
在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是________，
CG和EH的数量关系是________，
的值是________．
(2)类比延伸：
如图2，在原题条件下，若＝m(m＞0)则的值是________(用含有m的代数式表示)，试写出解答过程．
(3)拓展迁移：
如图3，梯形ABCD中，DC∥AB，点E是BC的延长线上的一点，AE和BD相交于点F，若
＝a，
＝b(a＞0，b＞0)则
的值是________(用含a、b的代数式表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一次夏令营活动中，小明从营地A出发，沿北偏东60°方向走了
m 到达点B，然后再沿北偏西30°方向走了50m到达目的地C。
（1）求A、C两点之间的距离；
（2）确定目的地C在营地A的北偏东多少度方向。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点N沿路线O→A→C运动.
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）当△ONC的面积是△OAC面积的
时，求出这时点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
三个顶点的坐标分别为
，
，
。
（1）请画出关于
轴对称后得到的
；
（2）直接写出点
，点
，点
的坐标；
（3）在
轴上寻找一个点
，使
的周长最小，并直接写出的周长的最小值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=x2﹣（m+1）x+m
（1）求证：抛物线与x轴一定有交点；
（2）若抛物线与x轴交于A（x1，0），B（x2，0）两点，x1＜0＜x2，且
，求m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
