
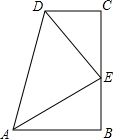
 已知:如图,∠B=∠C=90°,∠ADC的平分线交BC于E点,连AE,若AD=DC+AB,求∠AED的度数.
已知:如图,∠B=∠C=90°,∠ADC的平分线交BC于E点,连AE,若AD=DC+AB,求∠AED的度数. 分析 先构造出全等三角形,得出∠DEM=∠DEC ①,∠DME=∠C=90°,进而用HL判断出Rt△AME≌Rt△ABE,即可得出结论.
解答 解:如图,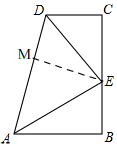
在AD上取点M,使得DM=DC,
∵∠ADC的平分线交BC于E点,
∴∠MDE=∠CDE,
在△DME和△DCE中,$\left\{\begin{array}{l}{DM=DC}\\{∠MDE=∠CDE}\\{DE=DE}\end{array}\right.$
∴△DME≌△DCE,
∴∠DEM=∠DEC ①,∠DME=∠C=90°,
∵∠B=∠C=90°,
∴∠AEE=∠B
∵DM=DC,AD=DC+AB,
∴AM=AB,
在Rt△AME和Rt△ABE中,$\left\{\begin{array}{l}{AE=AE}\\{AM=AB}\end{array}\right.$
∴Rt△AME≌Rt△ABE,
∴∠AEM=∠AEB②,
由①②可得∠AED=90°.
点评 此题是全等三角形的判定和性质,主要考查了角平分线的性质,解本题的关键是构造出△DME≌△DCE,也可以用角平分线的性质定理和判定定理直接计算出.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:单选题
若(x+y)2=9,(x﹣y)2=5,则xy的值为( )
A. ﹣1; B. 1 ; C. ﹣4; D. 4
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:解答题
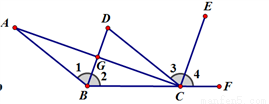
如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com