
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЁїBADКЭЁїBCEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯBAD=ЁЯBCE=90ЁуЃЌЕуMЮЊDEЕФжаЕуЃЎЙ§ЕуEгыADЦНааЕФжБЯпНЛЩфЯпAMгкЕуNЃЎ
ЃЈ1ЃЉЕБAЃЌBЃЌCШ§ЕудкЭЌвЛжБЯпЩЯЪБЃЈШчЭМ1ЃЉЃЌЧѓжЄЃКMЮЊANЕФжаЕуЃЛ
ЃЈ2ЃЉНЋЭМ1жаЁїBCEШЦЕуBа§зЊЃЌЕБAЃЌBЃЌEШ§ЕудкЭЌвЛжБЯпЩЯЪБЃЈШчЭМ2ЃЉЃЌЧѓжЄЃКЁїCANЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉНЋЭМ1жаЁїBCEШЦЕуBа§зЊЕНЭМ3ЕФЮЛжУЪБЃЌ(2)жаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЪджЄУїжЎЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
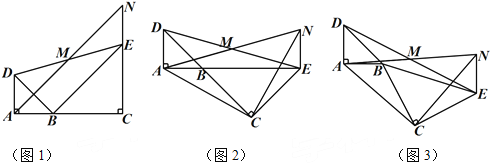
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЁїACNШдЮЊЕШбќжБНЧШ§НЧаЮЃЎжЄУїМћНтЮіЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩENЁЮADКЭЕуMЮЊDEЕФжаЕуПЩвджЄЕНЁїADMЁеЁїNEMЃЌДгЖјжЄЕНMЮЊANЕФжаЕуЃЎ
ЃЈ2ЃЉвзжЄAB=DA=NEЃЌЁЯABC=ЁЯNEC=135ЁуЃЌДгЖјПЩвджЄЕНЁїABCЁеЁїNECЃЌНјЖјПЩвджЄЕНAC=NCЃЌЁЯACN=ЁЯBCE=90ЁуЃЌдђгаЁїACNЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ3ЃЉбгГЄABНЛNEгкЕуFЃЌвзЕУЁїADMЁеЁїNEMЃЌИљОнЫФБпаЮBCEFФкНЧКЭЃЌПЩЕУЁЯABC=ЁЯFECЃЌДгЖјПЩвджЄЕНЁїABCЁеЁїNECЃЌНјЖјПЩвджЄЕНAC=NCЃЌЁЯACN=ЁЯBCE=90ЁуЃЌдђгаЁїACNЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌ
ЁпENЁЮADЃЌ
ЁрЁЯMAD=ЁЯMNEЃЌЁЯADM=ЁЯNEMЃЎ
ЁпЕуMЮЊDEЕФжаЕуЃЌ
ЁрDM=EMЃЎ
дкЁїADMКЭЁїNEMжаЃЌ
Ёр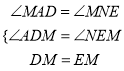 ЃЎ
ЃЎ
ЁрЁїADMЁеЁїNEMЃЎ
ЁрAM=MNЃЎ
ЁрMЮЊANЕФжаЕуЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌ
ЁпЁїBADКЭЁїBCEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAB=ADЃЌCB=CEЃЌЁЯCBE=ЁЯCEB=45ЁуЃЎ
ЁпADЁЮNEЃЌ
ЁрЁЯDAE+ЁЯNEA=180ЁуЃЎ
ЁпЁЯDAE=90ЁуЃЌ
ЁрЁЯNEA=90ЁуЃЎ
ЁрЁЯNEC=135ЁуЃЎ
ЁпAЃЌBЃЌEШ§ЕудкЭЌвЛжБЯпЩЯЃЌ
ЁрЁЯABC=180ЁуЉЁЯCBE=135ЁуЃЎ
ЁрЁЯABC=ЁЯNECЃЎ
ЁпЁїADMЁеЁїNEMЃЈвбжЄЃЉЃЌ
ЁрAD=NEЃЎ
ЁпAD=ABЃЌ
ЁрAB=NEЃЎ
дкЁїABCКЭЁїNECжаЃЌ
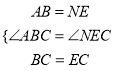
ЁрЁїABCЁеЁїNECЃЎ
ЁрAC=NCЃЌЁЯACB=ЁЯNCEЃЎ
ЁрЁЯACN=ЁЯBCE=90ЁуЃЎ
ЁрЁїACNЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ3ЃЉЁїACNШдЮЊЕШбќжБНЧШ§НЧаЮЃЎ
жЄУїЃКШчЭМ3ЃЌбгГЄABНЛNEгкЕуFЃЌ
ЁпADЁЮNEЃЌMЮЊжаЕуЃЌ
ЁрвзЕУЁїADMЁеЁїNEMЃЌ
ЁрAD=NEЃЎ
ЁпAD=ABЃЌ
ЁрAB=NEЃЎ
ЁпADЁЮNEЃЌ
ЁрAFЁЭNEЃЌ
дкЫФБпаЮBCEFжаЃЌ
ЁпЁЯBCE=ЁЯBFE=90Ёу
ЁрЁЯFBC+ЁЯFEC=360ЁуЉ180Ёу=180Ёу
ЁпЁЯFBC+ЁЯABC=180Ёу
ЁрЁЯABC=ЁЯFEC
дкЁїABCКЭЁїNECжаЃЌ
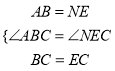
ЁрЁїABCЁеЁїNECЃЎ
ЁрAC=NCЃЌЁЯACB=ЁЯNCEЃЎ
ЁрЁЯACN=ЁЯBCE=90ЁуЃЎ
ЁрЁїACNЮЊЕШбќжБНЧШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
(1)(Ѓ2xy)(3x2Ѓ2xyЃ4y2)ЃЛ
(2)(Ѓ![]() m2nЃ
m2nЃ![]() mnЃЋ1)ЁЄ(Ѓ6m3n)ЃЛ
mnЃЋ1)ЁЄ(Ѓ6m3n)ЃЛ
(3)(Ѓ3x2y)2ЁЄ(Ѓ4xy2Ѓ5y3Ѓ6xЃЋ1)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛИіГЄ5mЕФЬнзгABЃЌаБППдквЛЪњжБЕФЧНAOЩЯЃЌетЪБAOЕФОрРыЮЊ4mЃЌШчЙћЬнзгЕФЖЅЖЫAбиЧНЯТЛЌ1mжСCЕуЃЎ
ЃЈ1ЃЉЧѓЬнзгЕзЖЫBЭтвЦОрРыBDЕФГЄЖШЃЛ
ЃЈ2ЃЉВТЯыCEгыBEЕФДѓаЁЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BC=4ЃЌЕуDЮЊABЕФжаЕуЃЌMЃЌNЗжБ№дкBCЃЌACЩЯЃЌЧвBM=CNЯжгавдЯТЫФИіНсТлЃК
ЂйDN=DMЃЛ Ђк ЁЯNDM=90ЁуЃЛ Ђл ЫФБпаЮCMDNЕФУцЛ§ЮЊ4ЃЛ ЂмЁїCMNЕФУцЛ§зюДѓЮЊ2.
Цфжае§ШЗЕФНсТлгаЃЈ ЃЉ

A. ЂйЂкЂмЃЛ B. ЂйЂкЂлЃЛ C. ЂкЂлЂмЃЛ D. ЂйЂкЂлЂм.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДЯДЯЪЧвЛЮЛЗЧГЃЯВЛЖЖЏФдНюЕФГѕвЛбЇЩњЃЌЬиБ№ЪЧбЇСЫМИКЮКѓЃЌИќОѕЕУЪ§бЇЦцУюЃЌЕБДЯДЯбЇЭъ![]() ЭМаЮЕФГѕВНжЊЪЖ
ЭМаЮЕФГѕВНжЊЪЖ![]() КѓЖдНЧЦНЗжЯпаЫШЄИќХЈКёЃЌЯТУцЧыФуКЭДЯДЯЭЌбЇвЛЦ№РДЬНОПЦцУюЕФНЧЦНЗжЯпАЩ
КѓЖдНЧЦНЗжЯпаЫШЄИќХЈКёЃЌЯТУцЧыФуКЭДЯДЯЭЌбЇвЛЦ№РДЬНОПЦцУюЕФНЧЦНЗжЯпАЩ![]() вбжЊ
вбжЊ![]() ЃЌЩфЯпOEЃЌOFЗжБ№ЪЧ
ЃЌЩфЯпOEЃЌOFЗжБ№ЪЧ![]() КЭ
КЭ![]() ЕФНЧЦНЗжЯпЃЎ
ЕФНЧЦНЗжЯпЃЎ
![]() ШчЭМ1ЃЌШєЩфЯпOCдк
ШчЭМ1ЃЌШєЩфЯпOCдк![]() ЕФФкВПЃЌЧв
ЕФФкВПЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
![]() ШчЭМ2ЃЌШєЩфЯпOCдк
ШчЭМ2ЃЌШєЩфЯпOCдк![]() ЕФФкВПШЦЕуOа§зЊЃЌЧв
ЕФФкВПШЦЕуOа§зЊЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
![]() ШєЩфЯпOCдк
ШєЩфЯпOCдк![]() ЕФЭтВПШЦЕуOа§зЊ
ЕФЭтВПШЦЕуOа§зЊ![]() а§зЊжа
а§зЊжа![]() ЃЌ
ЃЌ![]() ОљжИаЁгк
ОљжИаЁгк![]() ЕФНЧ
ЕФНЧ![]() ЃЌЦфгрЬѕМўВЛБфЃЌЧыНшжњЭМ3ЬНОП
ЃЌЦфгрЬѕМўВЛБфЃЌЧыНшжњЭМ3ЬНОП![]() ЕФДѓаЁЃЌЧыжБНгаДГі
ЕФДѓаЁЃЌЧыжБНгаДГі![]() ЕФЖШЪ§
ЕФЖШЪ§![]() ВЛаДЬНОПЙ§ГЬ
ВЛаДЬНОПЙ§ГЬ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЪагавЛПщГЄЮЊЃЈ3a+bЃЉУзЃЌПэЮЊЃЈ2a+bЃЉУзЕФГЄЗНаЮЕиПщЃЌжаМфЪЧБпГЄЮЊЃЈa+bЃЉУзЕФе§ЗНаЮЃЌЙцЛЎВПУХМЦЛЎНЋдкжаМфЕФе§ЗНаЮаоНЈвЛзљЕёЯёЃЌЫФжмЕФвѕгАВПЗжНјааТЬЛЏЃЌ
ЃЈ1ЃЉТЬЛЏЕФУцЛ§ЪЧЖрЩйЦНЗНУзЃПЃЈгУКЌзжФИaЁЂbЕФЪНзгБэЪОЃЉ
ЃЈ2ЃЉЧѓГіЕБaЃН20ЃЌbЃН12ЪБЕФТЬЛЏУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯгаСНЕуAЁЂBЃЌЕуAЖдгІЕФЪ§ЪЧ40ЃЌЕуBЖдгІЕФЪ§ЪЧ![]() ЃЎ
ЃЎ
![]() ЧѓЯпЖЮABЕФГЄЃЎ
ЧѓЯпЖЮABЕФГЄЃЎ
![]() ШчЭМ2ЃЌOБэЪОдЕуЃЌЖЏЕуPЁЂTЗжБ№ДгBЁЂOСНЕуЭЌЪБГіЗЂЯђзѓдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуAГіЗЂЯђгвдЫЖЏЃЌЕуPЁЂTЁЂQЕФЫйЖШЗжБ№ЮЊ5ИіЕЅЮЛГЄЖШ
ШчЭМ2ЃЌOБэЪОдЕуЃЌЖЏЕуPЁЂTЗжБ№ДгBЁЂOСНЕуЭЌЪБГіЗЂЯђзѓдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуAГіЗЂЯђгвдЫЖЏЃЌЕуPЁЂTЁЂQЕФЫйЖШЗжБ№ЮЊ5ИіЕЅЮЛГЄЖШ![]() УыЁЂ1ИіЕЅЮЛГЄЖШ
УыЁЂ1ИіЕЅЮЛГЄЖШ![]() УыЁЂ2ИіЕЅЮЛГЄЖШ
УыЁЂ2ИіЕЅЮЛГЄЖШ![]() УыЃЌЩшдЫЖЏЪБМфЮЊtЃЎ
УыЃЌЩшдЫЖЏЪБМфЮЊtЃЎ
![]() ЧѓЕуPЁЂTЁЂQБэЪОЕФЪ§
ЧѓЕуPЁЂTЁЂQБэЪОЕФЪ§![]() гУКЌгаtЕФДњЪ§ЪНБэЪО
гУКЌгаtЕФДњЪ§ЪНБэЪО![]() ЃЛ
ЃЛ
![]() дкдЫЖЏЙ§ГЬжаЃЌШчЙћЕуMЮЊЯпЖЮPTЕФжаЕуЃЌЕуNЮЊЯпЖЮOQЕФжаЕуЃЌЪдЫЕУїдкдЫЖЏЙ§ГЬжаЕШСПЙиЯЕ
дкдЫЖЏЙ§ГЬжаЃЌШчЙћЕуMЮЊЯпЖЮPTЕФжаЕуЃЌЕуNЮЊЯпЖЮOQЕФжаЕуЃЌЪдЫЕУїдкдЫЖЏЙ§ГЬжаЕШСПЙиЯЕ![]() ЪМжеГЩСЂЃЎ
ЪМжеГЩСЂЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЙФРјЪаУёНкдМгУЫЎЃЌЮвЪаОгУёЪЙгУздРДЫЎМЦЗбЗНЪНЪЕЪЉНзЬнЫЎМлЃЌОпЬхБъзММћБэ1ЃЌБэ2ЗжБ№ЪЧаЁУїЁЂаЁРіЁЂаЁБѓЁЂаЁгюЫФМв2017ФъЕФФъгУЫЎСПКЭНЩФЩЫЎЗбЧщПіЃЎ
Бэ1ЃКДѓСЌЪаОгУёздРДЫЎЪЕЪЉНзЬнЫЎМлБъзМЧщПіЃК
НзЬн | УПЛЇФъгУЫЎСПЃЈСЂЗНУзЃЉ | ЫЎМлЃЈКЌЮлЫЎДІРэЗбЃЉЃЈдЊ/СЂЗНУзЃЉ |
ЕквЛНзЬн | 0ЁЋmЃЈКЌmЃЉ | a |
ЕкЖўНзЬн | mЁЋ240ЃЈКЌ240ЃЉ | 4.40 |
ЕкШ§НзЬн | 240вдЩЯ | 7.85 |
Бэ2ЃКЫФИіМвЭЅ2017ФъЕФФъгУЫЎСПКЭНЩФЩЫЎЗбЧщПіЃК
МвЭЅ | аЁУї | аЁРі | аЁБѓ | аЁгю |
гУЫЎСПЃЈСЂЗНУзЃЉ | 50 | 100 | 200 | 220 |
ЫЎЗбЃЈдЊЃЉ | 162.5 | 325 | 673 | 761 |
ЧыФуИљОнБэ1ЁЂБэ2ЬсЙЉЕФЪ§ОнЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіБэ1жаЕФaЃЌmЕФжЕЃЛ
ЃЈ2ЃЉаЁгБМв2017ФъЪЙгУздРДЫЎЙВНЩФЩЫЎЗб827дЊЃЌдђЫ§Мв2017ФъЕФФъгУЫЎСПЪЧЖрЩйСЂЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
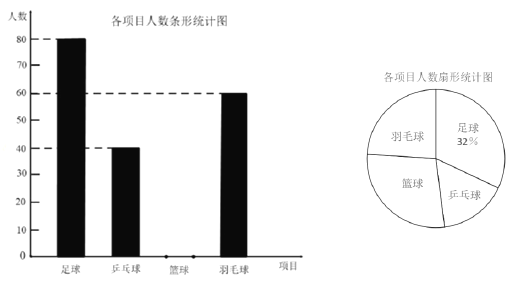
ЁОЬтФПЁПФГбЇаЃОйааЁАУПЬьЖЭСЖвЛаЁЪБЃЌНЁПЕЩњЛювЛБВзгЁБЮЊжїЬтЕФЬхг§ЛюЖЏЃЌВЂПЊеЙСЫвдЯТЬхг§ЯюФПЃКзуЧђЁЂЦЙХвЧђЁЂРКЧђКЭг№УЋЧђЃЌвЊЧѓУПЮЛбЇЩњБиаыЧвжЛФмбЁдёвЛЯюЁЃЮЊСЫНтбЁдёИїЯюЬхг§ЛюЖЏЕФбЇЩњШЫЪ§ЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂНЋЛёЕУЕФЪ§ОнНјааећРэЃЌЛцжЦГівдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭГМЦЭМЛиД№ЮЪЬтЃК
ЃЈ1ЃЉетДЮЛюЖЏвЛЙВЕїВщСЫ УћбЇЩњЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЧѓбЁдёРКЧђЯюФПЕФШЫЪ§дкЩШаЮЭГМЦЭМжаЫљеМЕФАйЗжБШЃП
ЃЈ4ЃЉШєИУбЇаЃга1500ШЫЃЌЧыФуЙРМЦИУбЇаЃбЁдёЦЙХвЧђЯюФПЕФбЇЩњШЫЪ§дМЪЧЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com