
 如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.
如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标. 分析 分两种情况:①当F在直线AB的上方时,即为F1,作辅助线,构建直角三角形,设F1(a,-10a+60),则EG=a-1,F1G=-10x+60-2,先证明△AEM∽△DNE,得$\frac{EM}{NE}=\frac{1}{2}$,再证明△MEN∽△EGF,列比例式可求得点F1的坐标;
②当F在直线AB的下方时,即为F2,同理证明相似并得比例式,求出F的坐标.
解答 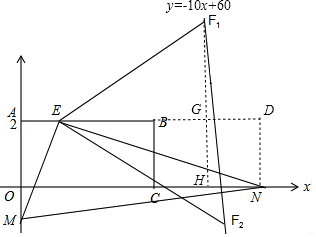 解:如图,画出直线F1F2:y=-10x+60,
解:如图,画出直线F1F2:y=-10x+60,
分两种情况:①当F在直线AB的上方时,即为F1,
延长AB,过F1作F1H⊥x轴于H,交AB的延长线于G,过N作DN⊥x轴,交AB的延长线于D,
设F1(a,-10a+60),则EG=a-1,F1G=-10x+60-2,
∵∠MEN=90°,
∴∠AEM+∠BEN=90°,
∵∠OAB=90°,
∴∠AEM+∠AME=90°,
∴∠BEM=∠AME,
∵∠OAB=∠EDN=90°,
∴△AEM∽△DNE,
∴$\frac{EM}{NE}=\frac{AE}{DN}$,
∵E(1,2),
∴AE=1,DN=2,
∴$\frac{EM}{NE}=\frac{1}{2}$,
∵∠BEF=∠EMN,∠MEN=∠EGF=90°,
∴△MEN∽△EGF,
∴$\frac{ME}{EN}=\frac{EG}{GF}$=$\frac{1}{2}$,
∴$\frac{a-1}{-10a+60-2}$=$\frac{1}{2}$,
a=5,
∴-10a+60=10,
∴F1(5,10);
②当F在直线AB的下方时,即为F2,
同理得:$\frac{10a-60+2}{a-1}$=$\frac{2}{1}$,
a=7,
当a=7时,-10a+60=-10,
∴F2(7,-10),
综上所述,点F的坐标为(5,10)或(7,-10).
点评 本题考查了一次函数图象上点的坐标的特征和矩形的性质,并与相似结合,根据坐标得出线段的长,利用相似列比例式,求出点F的坐标,同时采用了分类讨论的思想,属于易错题,容易丢解,注意点F在直线AB的下方时纵坐标与边长的关系.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知抛物线y=-3(x+m)2+k与x轴交于A(1,0),B(3,0)两点,现将抛物线向左平移,记平移后的抛物线顶点为C′,当点C′恰好落在y轴上时,平移后的抛物线解析式为y=-3(x-2)2.
如图,已知抛物线y=-3(x+m)2+k与x轴交于A(1,0),B(3,0)两点,现将抛物线向左平移,记平移后的抛物线顶点为C′,当点C′恰好落在y轴上时,平移后的抛物线解析式为y=-3(x-2)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
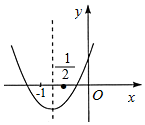 二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com