
【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB= ![]() .
.
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
【答案】
(1)解:①∵点B的坐标为(6,0),tan∠OCB= ![]() ,
,
∴BC=10,OC=8,
设直线BC的解析式为y=kx+b,
![]() ,
,
解得 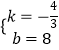 ,
,
∵点Q的横坐标为m,
∴点Q的纵坐标为﹣ ![]() m+8;
m+8;
②如图1,作OQ⊥AB交⊙A于P,则此时PQ最小, 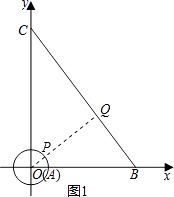
![]() ×AB×OQ=
×AB×OQ= ![]() ×BO×CO,
×BO×CO,
解得,OQ=4.8,
∴PQ最小=OQ最小﹣1=3.8;
(2)解:①如图2,⊙A与直线BC相切于H,
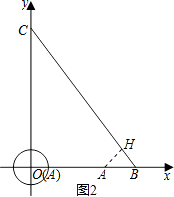
则AH⊥BC,又∠BOC=90°,
∴△BHA∽△BOC,
∴ ![]() ,即
,即 ![]() ,
,
解得,BA= ![]() ,
,
则OA=6﹣ ![]() =
= ![]() ,
,
∴t= ![]() 时,⊙A与直线BC相切;
时,⊙A与直线BC相切;
②由(2)①得,t= ![]() 时,⊙A与直线BC相切,
时,⊙A与直线BC相切,
当t=5时,⊙A经过点B,
当t=7时,⊙A经过点B,
当t=15时,⊙A经过点C,
故 ![]() <t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
<t≤5或7≤t≤15时,⊙A与线段BC有两个公共点.
【解析】(1)①根据待定系数法确定直线BC的解析式,即写出Q点的纵坐标。②作OQ⊥AB交⊙A于P,则此时PQ最小,根据两点之间线段最短进行分析。
(2)①根据相切得垂直,即可得出△BHA∽△BOC,然后求出AB的长,得OA的长,即可得出时间t;②由点动带动图形动,对题意进行分析,有两个交点即分类型讨论,由正好一个交点,过渡到正好两个交点的方式思考。
【考点精析】本题主要考查了确定一次函数的表达式和直线与圆的三种位置关系的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于 ![]() 的一元二次方程m
的一元二次方程m ![]() +2x-1=0有两个不相等的实数根,则
+2x-1=0有两个不相等的实数根,则 ![]() 的取值范围是( )
的取值范围是( )
A.m<-1
B.m>1
C.m<1且m≠0
D.m>-1且m≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
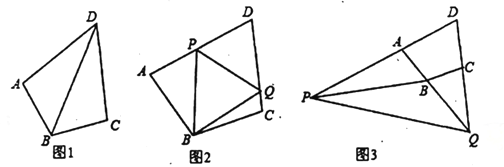
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() .
.
(1)如图1.连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,满足
上,满足![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短![]() 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程
如图,OA、BC分别是普通列车和动车从盐城开往北京的路程![]() 与时间
与时间![]() 的函数图象
的函数图象![]() 请根据图中的信息,解答下列问题:
请根据图中的信息,解答下列问题:
![]() 根据图象信息,普通列车比动车早出发______h,动车的平均速度是______
根据图象信息,普通列车比动车早出发______h,动车的平均速度是______![]() ;
;
![]() 分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
![]() 动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
动车出发多少小时追上普通列车?此时他们距离出发地多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.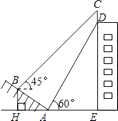
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 ![]() 米.
米.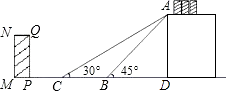
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com