
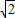 CE+PC的值不变.
CE+PC的值不变.
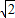 CE,因此所求的结论可转化为证PM是否为定值,观察图形,可通过证△PEM、△BEC是否全等来判断.
CE,因此所求的结论可转化为证PM是否为定值,观察图形,可通过证△PEM、△BEC是否全等来判断.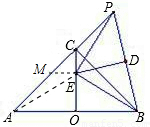
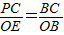 ,即PC•OB=OE•BC?PC•OA=OE•BC;
,即PC•OB=OE•BC?PC•OA=OE•BC;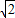 EC,∠PME=45°;
EC,∠PME=45°;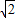 EC+PC,所以
EC+PC,所以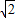 CE+PC的值不变,故④正确;
CE+PC的值不变,故④正确;

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
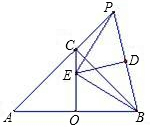 如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )| 2 |
| ||
| 2 |
查看答案和解析>>
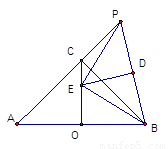
科目:初中数学 来源:2011-2012学年浙江省义乌市初中毕业生学业模拟考试数学试卷(解析版) 题型:选择题
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一
个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:
①E为△ABP的外心; ②△PBE为等腰直角三角形;
③PC·OA = OE·PB; ④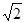 CE + PC的值不变.
CE + PC的值不变.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市中考数学模拟试卷(23)(解析版) 题型:选择题
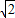 CE+PC的值不变.
CE+PC的值不变.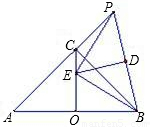
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com