
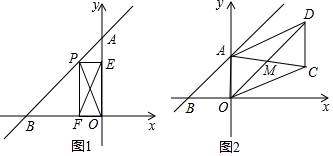
分析 (1)由已知条件定点y=x+5,令y=0,则x=-5,令x=0,则y=5,于是得到结论;
(2)①由(1)得,OB=5,由于P(m,n)在直线AB上,得到n=m+5,求得PF=m+5,根据三角形的面积公式即可得到结论;②存在根据矩形的性质得到EF=OP,得到当OP⊥AB时,OP取得最小值,由(1)知,OA=OB,根据等腰三角形的性质得到EF的最小值是$\frac{5}{2}$$\sqrt{2}$;
(3)①根据旋转的性质得到AM=CM,OM=DM,根据平行四边形的判定定理得到四边形AOCD的是平行四边形;②由四边形AOCD是正方形,得到AO⊥OC,根据AO⊥x轴,得到OC在x轴上,推出CD⊥x轴,根据点M(3,3),OM=DM,得到D(6,6),于是得到结论.
解答 解:(1)当b=5时,即直线AB的解析式为y=x+5,
令y=0,则x=-5,令x=0,则y=5,
∴A(0,5),B(-5,0),
故答案为:0,5,-5,0;
(2)①由(1)得,OB=5,
∵P(m,n)在直线AB上,
∴n=m+5,
∴PF=m+5,
∴S△PBO=$\frac{1}{2}$OB•PF,
∴S=$\frac{5}{2}$(m+5)=$\frac{5}{2}$m+$\frac{25}{2}$(-5≤m≤0);
②存在,∵∠PFO=∠FOE=∠OEP=90°,
∴四边形PFOE是矩形,
∴EF=OP,
∵O为定点,P在直线AB上运动,
∴当OP⊥AB时,OP取得最小值,
由(1)知,OA=OB,
当OP⊥AB时,PA=PB,
∴OP=$\frac{1}{2}$AB,
∵AB=5$\sqrt{2}$,
∴OP=$\frac{5}{2}$$\sqrt{2}$,
∴EF的最小值是$\frac{5}{2}$$\sqrt{2}$,
此时,S=$\frac{25}{4}$;
(3)①∵将△AOM绕点M旋转180°得到△CDM,
∴AM=CM,OM=DM,
∴四边形AOCD的是平行四边形;
②∵四边形AOCD是正方形,
∴AO⊥OC,
∵AO⊥x轴,
∴OC在x轴上,
∵AO∥CD,
∴CD⊥x轴,
∵点M(3,3),OM=DM,
∴D(6,6),
∴CD=6,
∴OA=6,
∴b=6,
故答案为:平行四边形,6.
点评 本题考查了一次函数的性质,一次函数图象上点的坐标特征,三角形面积的计算,平行四边形的判定,正方形的性质,旋转的性质,正确的理解题意是解题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)
如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20cm | B. | 24cm | C. | 28cm | D. | 30cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=kx+b经过点A(-2,-4)和点B(-5,0),直线y=2x过点A,则不等式2x<kx+b的解集为( )
如图,直线y=kx+b经过点A(-2,-4)和点B(-5,0),直线y=2x过点A,则不等式2x<kx+b的解集为( )| A. | x<-5 | B. | x<-2 | C. | x>-5 | D. | x>-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
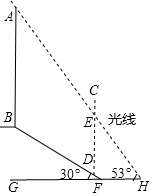 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )| A. | 35.5米 | B. | 37.6米 | C. | 38.6米 | D. | 40.3米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com