
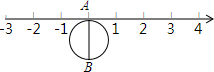
分析 (1)直接利用圆周长公式结合数轴得出答案;
(2)①直接利用滚动方向和滚动周数结合数轴得出答案;
②直接利用滚动方向和滚动周数结合数轴得出答案.
解答 解:(1)∵半径为1个单位的圆片上有一点A与数轴上的原点重合,把圆片沿数轴向左滚动半周,点B到达数轴上点C的位置,
∴点C表示的数是:无理数,这个数是:-π;
故答案为:无理数,-π;
(2)①∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,
依次运动情况记录如下:+2,-1,+4,-6,+3,
∴第3次滚动后,A点距离原点最远,为5周的距离,
②∵2-1+4-6+3=2,
∴圆向右滚动了2周,
∴当圆片结束运动时,此时点A所表示的数是:2π×1×2=4π.
故答案为:3;4π.
点评 此题主要考查了数轴以及正数和负数以及圆周长公式,正确得出圆的滚动位置是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
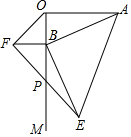 如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为2.
如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
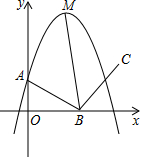 如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).
如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3≤x≤3 | B. | 0≤x≤3 | C. | 0<x≤3 | D. | x>3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com