
【题目】如图,已知⊙O 的半径长为2,点C为直径AB的延长线上一点,且BC=2.过点C任作一条直线l.若直线l上总存在点P,使得过点P所作的⊙O 的两条切线互相垂直,则∠ACP的最大值等于__________°.

【答案】45
【解析】
根据切线的性质和已知条件先证得四边形PMON是正方形,从而求得OP= ![]() ,以O为圆心,以
,以O为圆心,以![]() 长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,作出图形,根据切线的性质得出OP⊥PC,根据勾股定理求得PC的长,从而证得△OPC是等腰直角三角形,即可证得∠ACP的最大值为45°.
长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,作出图形,根据切线的性质得出OP⊥PC,根据勾股定理求得PC的长,从而证得△OPC是等腰直角三角形,即可证得∠ACP的最大值为45°.
∵PM、PN是过P所作的⊙O的两切线且互相垂直,
∴∠MON=90°,
∴四边形PMON是正方形,
根据勾股定理求得![]() ,
,
∴P点在以O为圆心,以![]() 长为半径作大圆⊙O上,
长为半径作大圆⊙O上,
以O为圆心,以![]() 长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,如图所示,
长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,如图所示,
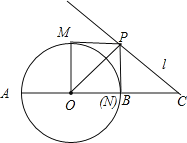 ,
,
∵PC是大圆⊙O的切线,
∴OP⊥PC,∵OC=4,OP= ![]() ,
,
∴PC= ![]() ,
,
∴OP=PC,
∴∠ACP=45°,
∴∠ACP的最大值等于45°.故答案为45.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2017年,我市某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年平均下调10%后.
(1)求2019年我市楼盘以每平方米多少元的均价对外销售?
(2)假设2020年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.(点
两点.(点![]() 在点
在点![]() 的左侧)
的左侧)
(1)①填空:![]() 时,点
时,点![]() 的坐标 ,点
的坐标 ,点![]() 的坐标 ;当
的坐标 ;当![]() 时,点
时,点![]() 的坐标 ,点
的坐标 ,点![]() 的坐标 .
的坐标 .
②猜想:随![]() 值的变化,抛物线
值的变化,抛物线![]() 是否会经过某一个定点,若会,请求出该定点的坐标:若不会,请说明理由.
是否会经过某一个定点,若会,请求出该定点的坐标:若不会,请说明理由.
(2)若将抛物线![]() 经过适当平移后,得到抛物线
经过适当平移后,得到抛物线![]() :
:![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,求抛物线
,求抛物线![]() 的解析式.
的解析式.
(3)设抛物线![]() 的顶点为
的顶点为![]() ,当
,当![]() 为直角三角形时,求方程
为直角三角形时,求方程![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
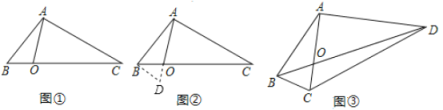
某学校数学社团遇到这样一个题目:如图①,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() ,如图②所示,通过构造
,如图②所示,通过构造![]() 就可以解决问题.
就可以解决问题.
请你写出求![]() 、
、![]() 的度数和求
的度数和求![]() 长的过程.
长的过程.
应用:
如图③,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]() 的长为 ,
的长为 ,![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E(即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.
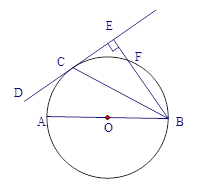
(1)求证:CD为⊙O的切线;
(2)若AB=10,CE=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长33米的竹篱笆围成一个矩形院墙,其中一面靠墙,墙长15米,墙的对面有一个2米宽的门,设垂直于墙的一边长为![]() 米,院墙的面积为
米,院墙的面积为![]() 平方米.
平方米.
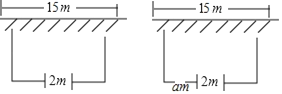
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若院墙的面积为143平方米,求![]() 的值;
的值;
(3)若在墙的对面再开一个宽为![]() 米的门,且面积
米的门,且面积![]() 的最大值为165平方米,求
的最大值为165平方米,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.

(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=2![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com