

 ····························· 1分
····························· 1分

 的周长之和为定值.··········································· 4分
的周长之和为定值.··········································· 4分 的周长之和等于BC+CH+BH
的周长之和等于BC+CH+BH  由AB=5,AM=4,可知
由AB=5,AM=4,可知  ,
, , △ECG的周长是
, △ECG的周长是
 的周长之和是24.
的周长之和是24.
 ···························· 8分
···························· 8分 .
. 时,y有最大值.···························································· 10分
时,y有最大值.···························································· 10分 .
.

 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源:不详 题型:单选题
 ( )
( ) 
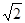 B.
B.  C.
C.  D.
D.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题



查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
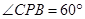 ,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是
,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是 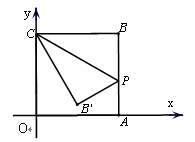
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
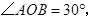 过
过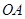 上到点
上到点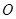 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作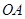 的垂线,分别与
的垂线,分别与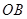 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为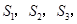 ….则
….则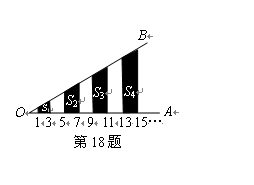
 ;
;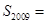 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com