
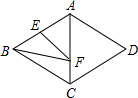
 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
分析 首先连接DB,DE,设DE交AC于M,连接MB,DF.证明只有点F运动到点M时,EF+BF取最小值,再根据菱形的性质、勾股定理求得最小值.
解答 解:连接DB,DE,设DE交AC于M,连接MB,DF,延长BA,DH⊥BA于H,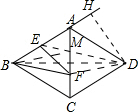 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC,BD互相垂直平分,
∴点B关于AC的对称点为D,
∴FD=FB,
∴FE+FB=FE+FD≥DE.
只有当点F运动到点M时,取等号(两点之间线段最短),
△ABD中,AD=AB,∠DAB=120°,
∴∠HAD=60°,
∵DH⊥AB,
∴AH=$\frac{1}{2}$AD,DH=$\frac{\sqrt{3}}{2}$AD,
∵菱形ABCD的边长为4,E为AB的中点,
∴AE=2,AH=2,
∴EH=4,DH=2$\sqrt{3}$,
在Rt△EHD中,DE=$\sqrt{E{H}^{2}+D{H}^{2}}$=2$\sqrt{7}$,
∴EF+BF的最小值为2$\sqrt{7}$.
故选D.
点评 此题主要考查菱形是轴对称图形的性质,知道什么时候会使EF+BF成为最小值是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
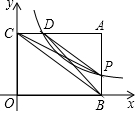 已知,A点的坐标为(4,3),过A点分别作坐标轴的垂线,交x轴和y轴分别于B点和C点,P为线段AB上一个动点(P不与A,B重合),过点P的反比例函数y=$\frac{k}{x}$的图象与AC交于点D.
已知,A点的坐标为(4,3),过A点分别作坐标轴的垂线,交x轴和y轴分别于B点和C点,P为线段AB上一个动点(P不与A,B重合),过点P的反比例函数y=$\frac{k}{x}$的图象与AC交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com