练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．设（3x-2）2=ax2+bx+c．求：
    （1）c的值
    （2）a+b+c的值．

    分析 将条件等式中的左边展开，利用等式的性质，即可求出a、b、c的值；

    解答 解：由题意可知：
    （3x-2）2=9x2-12x+4=ax2+bx+c
    ∴a=9，b=-12，c=4，
    ∴原式=9-12+4=1

    点评 本题考查完全平方公式，涉及代入求值，属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．计算：$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+$\frac{\frac{1}{3}}{（1+\frac{1}{2}）（1+\frac{1}{3}）}$+$\frac{\frac{1}{4}}{（1+\frac{1}{2}）（1+\frac{1}{3}）（1+\frac{1}{4}）}$+…+$\frac{\frac{1}{2016}}{（1+\frac{1}{2}）（1+\frac{1}{3}）…（1+\frac{1}{2016}）}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：2sin30°+3tan30°-tan45°-3tan60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若x=89，|y|=122，y＜0，则x+y=-33．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

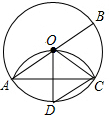    15．已知：如图，AB是⊙O的直径，AC是弦，将劣弧$\widehat{AC}$沿弦AC翻折与AB的交点恰好是圆心O，连接BC，作半径OD⊥AC．求证：四边形BCDO是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）（-82）3；
    （2）（am）2；
    （3）[（-m）3]4；
    （4）（a3-m）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）已知函数y=（m2-m）x2+（m-1）x+m+1，若这个函数是二次函数，求m的取值范围；
    （2）已知函数y=（m2+m）x${\;}^{{m}^{2}-2m-1}$是二次函数，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

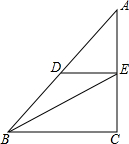    9．完成求解过程，并写出括号里的理由：
    如图，在直角△ABC中，∠C=90°，DE∥BC，BE平分∠ABC，∠ADE=40°，求∠BEC的度数．
    解：∵DE∥BC（已知）
    ∴∠ABC=∠ADE=40°
    ∵BE平分∠ABC（已知）
    ∴∠CBE=$\frac{1}{2}$∠ABC=20度
    ∵在Rt△ABC中，∠C=90°（已知）
    ∴∠BEC=90°-∠CBE=70度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，等腰△ABC中，AB=AC，BC∥x轴，点A、C在反比例函数y=$\frac{4}{x}$（x＞0）的图象上，点B在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，则△ABC的面积为$\frac{9}{10}$．

    查看答案和解析>>

    同步练习册答案