
自变量为x的二次函数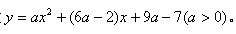
(1)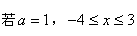 ,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
,求函数值y的最大值与最小值;并分别指出所对应的自变量x的值;
(2)当a变化时,该二次函数图象是否经过定点?若是,请求出定点坐标;若不是,请说明理由;
(3)若该二次函数图象与x轴有两个不同的交点,而且两交点的横坐标均小于-1,求a的取值范围。

【解析】(1)a值大于0,说明抛物线的开口向上;首先判断抛物线的对称轴是否在自变量的取值范围内,若在,那么顶点的纵坐标即为y的最小值;此时距抛物线对称轴最远点的纵坐标就是y的最大值.若不在,只需判断距抛物线对称轴的远近就能得出y的最大或最小值.可通过作图来辅助理解.
(2)将涉及a的项整理到一起,提取a后将含a的式子设为0(只有这样才能令a的值影响不到函数值),取得此时的自变量值后代入抛物线的解析式,即可判断出该抛物线是否经过某个定点.
(3)已知抛物线的开口向上、且与x轴的两个交点都在(-1,0)的左侧,那么当x=-1时,函数值一定大于0,可根据这个特点来确定a的取值范围.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省温州市育英学校九年级(上)月考数学试卷A班(9月份)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
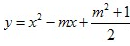 与
与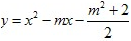 这两个二次函数的图象中的一个与x轴交于不同的两点A、B.
这两个二次函数的图象中的一个与x轴交于不同的两点A、B. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com