
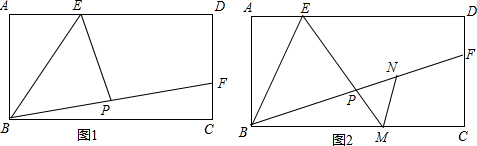
分析 如图,过点P作CD的平行线交BC于G,交AD于K,截取GH=AE,BM沿ME翻折至MR,过R作RQ⊥BC于Q,连结BR,BH,
(1)由题意得到PG垂直于BG,再由PG与FC平行,且P为BF中点,得到G为BC中点,得BC=2BG,由BC=2AB,得到AB=BG,利用SAS得到三角形ABE与三角形BGH全等,利用全等三角形对应角相等,对应边相等得到EB=BH,且∠ABE=∠HBG,利用等式的性质得到一对角相等,利用SAS得到三角形EBP与三角形HBP全等,利用全等三角形对应边、对应角相等得到∠BPE=∠BPH,EP=HP,由PG与DC平行,得到一对同位角相等,利用邻补角互补等量代换即可得证;
(2)以BC为x轴,AB为x轴,建立坐标系,如图所示,设BC=8a,AE=x,那么AK=AB=BG=KG=4a,EK=4a-x,继而表示出EK,KP,EP,在直角三角形EPK中,利用勾股定理表示出x,进而表示出EK,PK,根据∠RBM=∠EPK,得到tan∠RBM=tan∠EPK,求出RQ与BQ之比,进而设出RQ,BQ,在直角三角形RMQ中,利用勾股定理列出关系式,表示出RQ,BQ,进而表示出B,P,M,R坐标,利用待定系数法求出BF与RM解析式,联立表示出N坐标,求出PN与NF之比即可.
解答 解:如图,过点P作CD的平行线交BC于G,交AD于K,截取GH=AE,BM沿ME翻折至MR,过R作RQ⊥BC于Q,连结BR,BH,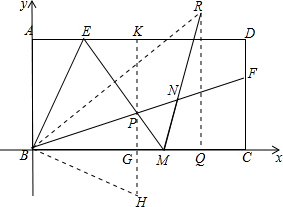
(1)∵KH∥AB,∠ABG=90°.
∴∠BGK=90°,即PG⊥BG,
∵BP=FP,PG∥FC,
∴BG=CG,即BC=2BG,
∵BC=2AB,
∴AB=BG,
在△BAE和△BGH中,
$\left\{\begin{array}{l}{BA=BG}\\{∠BAE=∠BGH}\\{AE=GH}\end{array}\right.$,
∴△BAE≌△BGH(SAS),
∴∠ABE=∠GBH,BE=BH,
∵∠ABG=90°,∠EBP=45°,
∴∠EBP=∠HBP=45°,
在△BEP和△BHP中,
$\left\{\begin{array}{l}{BE=BH}\\{∠EBP=∠HBP}\\{BP=BP}\end{array}\right.$,
∴△BEP≌△BHP(SAS),
∴∠BPE=∠BPH,EP=HP,
∵PG∥DC,
∴∠BPH=∠BFC,
∵∠BFC+∠BFD=180°,
∴∠BPE+∠DFP=180°;
(2)以BC为x轴,AB为x轴,建立坐标系,如图所示,
设BC=8a,AE=x,那么AK=AB=BG=KG=4a,EK=4a-x,
∵EP=2PM,EK∥GM,
∴KP=2PG=$\frac{8}{3}$a,PG=$\frac{4}{3}$a,EP=HP=PG+GH=AE+PG=x+$\frac{4}{3}$a,
∵在Rt△PEK中,根据勾股定理得:EK2+KP2=EP2,
∴(4a-x)2+($\frac{8}{3}$a)2=(x+$\frac{4}{3}$a)2,
∴x=2a,
∴EK=2a,GM=$\frac{1}{2}$EK=a,
∵∠RBM=∠EPK,
∴tan∠RBM=tan∠EPK,即$\frac{RQ}{BQ}$=$\frac{EK}{PK}$=$\frac{2a}{\frac{8}{3}a}$=$\frac{3}{4}$,
设RQ=3y,BQ=4y,BM=RM=BG+GM=4a+a=5a,
∴在Rt△RMQ中,根据勾股定理得:MQ2+RQ2=MR2,即(4y-5a)2+(3y)2=(5a)2,
∴y=$\frac{8}{5}$a,
∴BQ=$\frac{32}{5}$a,RQ=$\frac{24}{5}$a,
∴B(0,0),P(4a,$\frac{4}{3}$a),M(5a,0),R($\frac{32}{5}$a,$\frac{24}{5}$a),
可得直线BF解析式为:y=$\frac{1}{3}$x;直线MR解析式为:y=$\frac{24}{7}$x-$\frac{120}{7}$a,
令$\frac{1}{3}$x=$\frac{24}{7}$x-$\frac{120}{7}$,
解:x=$\frac{72}{13}$a,y=$\frac{24}{13}$a,
∴N($\frac{72}{13}$a,$\frac{24}{13}$a),
∴$\frac{PN}{NF}$=$\frac{\frac{72}{13}a-4a}{8a-\frac{72}{13}a}$=$\frac{5}{8}$.
点评 此题属于四边形综合题,涉及的知识有:全等三角形的判定与性质,锐角三角函数定义,待定系数法确定函数解析式,勾股定理,坐标与图形性质,折叠的性质,矩形的性质,熟练掌握性质与定理是解本题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
 某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
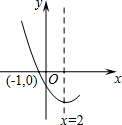 如图1,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为直线x=2,与x轴的一个交点是(-1,0);
如图1,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为直线x=2,与x轴的一个交点是(-1,0);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )
如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )| A. |  | B. |  | C. | 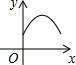 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
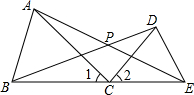 如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.
如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
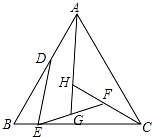 如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).
如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com