
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
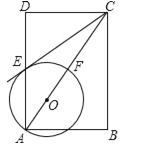
【答案】(1)相切
(2)![]()
【解析】试题(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC=![]() ,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(
,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(![]() -r) 2=r2+3,从而易得r的值;
-r) 2=r2+3,从而易得r的值;
试题解析:(1)直线CE与⊙O相切
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
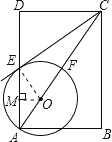
∵∠DCE+∠DEC=90°
∴∠AEO+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)∵tan∠ACB=![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB=![]() ,
,
∴AC=![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=![]() ,
,
∴DE=DCtan∠DCE=1;
在Rt△CDE中,CE=![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即(![]() -r) 2=r2+3
-r) 2=r2+3
解得:r=![]()


科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() ,
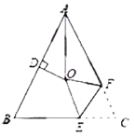
,![]() 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.去年当地每月的平均气温如图1,小明家去年月用电量如图2.
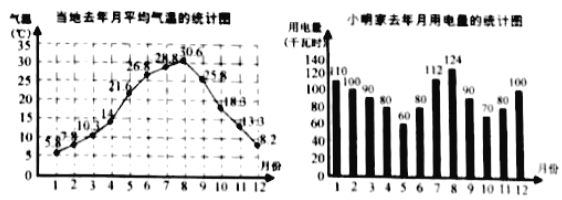
根据统计图,回答下面的问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
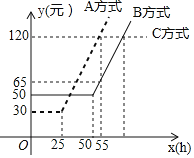
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
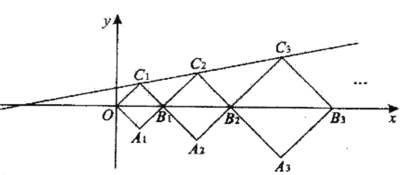
【题目】如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,···的顶点B1,B2,B3,···在x轴上,顶点C1,C2,C3···在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3, 则点C5的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
A、①②③B、①③⑤
C、②③④D、②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D.E分别是边AB、BC的中点,过点A作
,点D.E分别是边AB、BC的中点,过点A作![]() 交ED的延长线于点F,连接BF。
交ED的延长线于点F,连接BF。
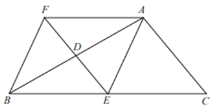
(1)求证:四边形ACEF是菱形;
(2)若四边形AEBF也是菱形,直接写出线段AB与线段AC的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
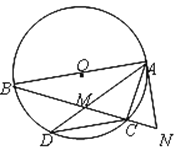
【题目】如图,△ABC内接于⊙O,AB为⊙O直径,AC=CD,连接AD交BC于点M,延长MC到N,使CN=CM.
(1)判断直线AN是否为⊙O的切线,并说明理由;
(2)若AC=10,tan∠CAD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
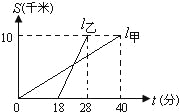
【题目】甲,乙两人以相同路线前往距离单位10![]() 的培训中心参加学习.图中
的培训中心参加学习.图中![]() 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s![]() 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8![]() 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com