
【题目】 如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点
(1)若AO=![]() ,求k的值;
,求k的值;
(2)若OQ长的最大值为![]() ,求k的值;
,求k的值;
(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.

【答案】(1)2;(2)![]() ;(3)a的值为-3或2或-4或1.
;(3)a的值为-3或2或-4或1.
【解析】
(1)设A(m,n),根据勾股定理和一次函数图象上点的坐标特征得出 ,解方程组即可求得A的坐标,代入y=
,解方程组即可求得A的坐标,代入y=![]() 可求得k的值;
可求得k的值;
(2)作辅助线,先确定OQ长的最大时,点P的位置,当BP过圆心C时,BP最长,设B(t,2t),则CD=t-(-2)=t+2,BD=-2t,根据勾股定理计算t的值,可得k的值;
(3)根据题意写出抛物线的解析式为:y=ax2+ax-2a=a(x+![]() )2-
)2-![]() a,即可判定-
a,即可判定-![]() 在a≤x≤a+1范围外,故存在两种可能,即当x=a时,有最大值4a,或x=a+1时有最大值4a,分别代入求得即可.
在a≤x≤a+1范围外,故存在两种可能,即当x=a时,有最大值4a,或x=a+1时有最大值4a,分别代入求得即可.
(1)设A(m,n),
∵AO=![]() ,
,
∴m2+n2=5,
∵一次函数y=2x的图象经过A点,
∴n=2m,
∴m2+(2m)2=5,解得m=±1,
∵A在第一象限,
∴m=1,
∴A(1,2),
∵点A在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=1×2=2;
(2)如图,连接BP,

由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=![]() BP,
BP,
∵OQ长的最大值为![]() ,
,
∴BP长的最大值为![]() ×2=3,
×2=3,
如图2,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t-(-2)=t+2,BD=-2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(t+2)2+(-2t)2,
t=0(舍)或-![]() ,
,
∴B(-![]() ,-
,-![]() ),
),
∵点B在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=-![]() ×(-
×(-![]() )=
)=![]() ;
;
(3)∵抛物线经过点C(-2,0),
∴4a-2b+c=0,
又∵a+b+c=0,
∴b=a,c=-2a,
∴y=ax2+ax-2a=a(x+![]() )2-
)2-![]() a,
a,
∵-![]() <a≤x≤a+1或a≤x≤a+1<-
<a≤x≤a+1或a≤x≤a+1<-![]() ,
,
当x=a时,取得最大值4a,
则aa2+aa-2a=4a,
解得a=-3或2,
当x=a+1时,取得最大值4a,
则a(a+1)2+a(a+1)-2a=4a,
解得a=-4或1,
综上所述所求a的值为-3或2或-4或1.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
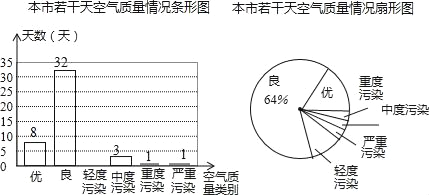
【题目】为了解哈市今年的空气质量情况,环保部门从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图不完整的统计图:
(1)计算被抽取的天数;
(2)请通过计算补全条形统计图;
(3)请估计哈市这一年(365天)达到优和良的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
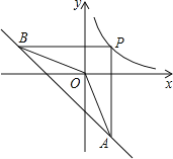
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的业余文化生活,某校教务处准备在大课间期间开设兴趣小组,预设科目为“舞蹈”“音乐”“电竞”“动漫”为了准确配备教室与师资,负责人制作了“你最喜欢的科目”的调查问卷,在校园随机调查后制作了两幅不完整的统计图,请你根据信息解答下面问题:
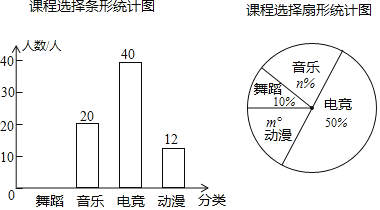
(1)本次调查中,参与问卷调查的人数为 ;
(2)扇形统计图中的m、n的值为 、 ,补全条形统计图;
(3)若该校有学生2000人,请你估计报名“电竞”的学生的人数为 ;
(4)最先报名“动漫”课程的三名学生中有两名男生一名女生,若随机抽取两名学生参与教室网线布设,求两名学生恰为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
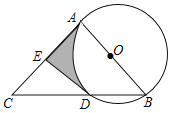
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,∠ACB=40°,AC=7.2,求图中阴影部分的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com