
 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$科目:初中数学 来源: 题型:填空题
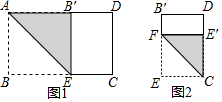 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
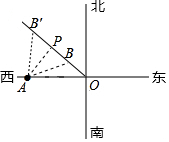 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
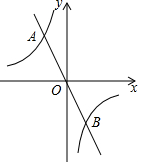 如图,在平面直角坐标系中,点A是第二象限内双曲线y=-$\frac{2}{x}$上一点,直线AO与双曲线的另一个交点为B.
如图,在平面直角坐标系中,点A是第二象限内双曲线y=-$\frac{2}{x}$上一点,直线AO与双曲线的另一个交点为B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com