
 如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,CD=8,则DE的长等于5.
如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,CD=8,则DE的长等于5. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.
如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
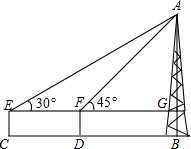 周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔AB前的平地上选择一点C,树立测角仪CE,测出看塔顶的仰角约为30°,从C点向塔底B走70米到达D点,测出看塔顶的仰角约为45°,已知测角仪器高为1米,则塔AB的高大约为($\sqrt{3}$≈1.7)( )
周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔AB前的平地上选择一点C,树立测角仪CE,测出看塔顶的仰角约为30°,从C点向塔底B走70米到达D点,测出看塔顶的仰角约为45°,已知测角仪器高为1米,则塔AB的高大约为($\sqrt{3}$≈1.7)( )| A. | 141米 | B. | 101米 | C. | 91米 | D. | 96米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com