
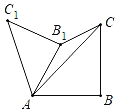
【题目】如图,△ABC为等腰直角三角形,∠B=90°,AB=2,把△ABC绕点A逆时针旋转60°得到△AB1C1,连接CB1,则点B1到直线AC的距离为_____.
【答案】![]() .
.
【解析】
连接CC1,过点B1作B1H⊥AC,由旋转的性质可得AC=AC1=2![]() ,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,可得∴△ACC1是等边三角形,由“SSS”可证△AB1C≌△C1B1C,可得S△AB1C=S△C1B1CS,由三角形的面积关系可求解.
,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,可得∴△ACC1是等边三角形,由“SSS”可证△AB1C≌△C1B1C,可得S△AB1C=S△C1B1CS,由三角形的面积关系可求解.
如图,连接CC1,过点B1作B1H⊥AC,
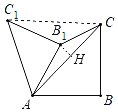
∵∠B=90°,AB=BC=2,
∴AC=2![]() ,
,
∵把△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2![]() ,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,
,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,
∴△ACC1是等边三角形,
∴C1C=AC,B1C=B1C,AB1=B1C1,
∴△AB1C≌△C1B1C(SSS)
![]()
![]()
∴![]() ×(2
×(2![]() )2=
)2=![]() ×2×2+2×
×2×2+2×![]() ×2
×2![]() ×B1H,
×B1H,
∴B1H=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】我们规定:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
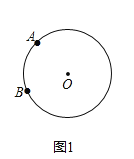
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
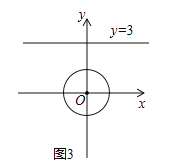
(2)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时PQ的长和点Q的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )
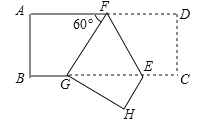
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b![]() )x+c=0的一个根;(4)当
)x+c=0的一个根;(4)当![]() <x<3时,ax2+(b
<x<3时,ax2+(b![]() )x+c>0.其中正确的个数为( )
)x+c>0.其中正确的个数为( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间满足关系:
(元)之间满足关系:![]() ,其图像如图所示.
,其图像如图所示.
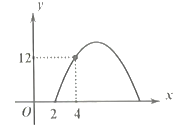
(1)销售单价为多少元时,这种商品每天的销售利润最大?最大利润为多少元?
(2)若该商品每天的销售利润不低于12元,则销售单价![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对函数y=﹣|x2﹣4|的图象和性质进行了探究,其探究过程中的列表如下:
x | … | -3 | ﹣2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 0 | -3 | n | -3 | 0 | -5 | … |
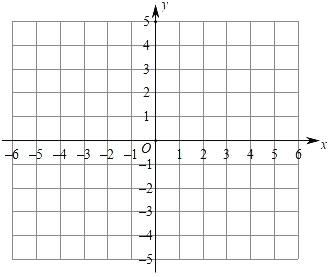
(1)求表中m,n的值;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)结合你所画的函数图象,直接写出不等式﹣|x2﹣4|>x﹣2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
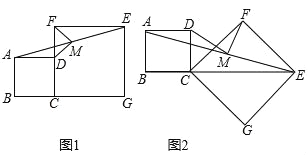
【题目】已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF,
(1)如图1,请直接给出线段MD、MF的数量及位置关系是 ;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
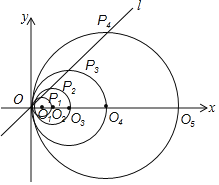
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com