
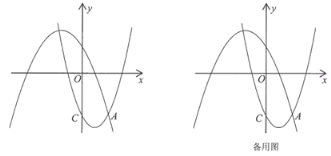
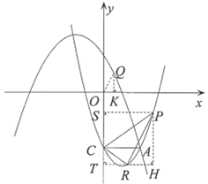
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
【答案】(1)抛物线![]() 对应的函数表达式为
对应的函数表达式为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;(3)点
;(3)点![]() 坐标为
坐标为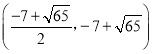 或
或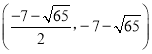 .
.
【解析】
(1)先求出A点的坐标,再用待定系数法求出函数解析式便可;
(2)设点P的坐标为(x,x2﹣2x﹣3),分两种情况讨论:AC为平行四边形的一条边,AC为平行四边形的一条对角线,用x表示出Q点坐标,再把Q点坐标代入抛物线![]() 中,列出方程求得解便可;
中,列出方程求得解便可;
(3)当点P在y轴左侧时,抛物线L1不存在点R使得CA平分∠PCR,当点P在y轴右侧时,不妨设点P在CA的上方,点R在CA的下方,过点P、R分别作y轴的垂线,垂足分别为S、T,过点P作PH⊥TR于点H,设点P坐标为(x1,![]() ),点R坐标为(x2,
),点R坐标为(x2,![]() ),证明△PSC∽△RTC,由相似比得到x1+x2=4,进而得tan∠PRH的值,过点Q作QK⊥x轴于点K,设点Q坐标为(m,
),证明△PSC∽△RTC,由相似比得到x1+x2=4,进而得tan∠PRH的值,过点Q作QK⊥x轴于点K,设点Q坐标为(m,![]() ),由tan∠QOK=tan∠PRH,移出m的方程,求得m便可.
),由tan∠QOK=tan∠PRH,移出m的方程,求得m便可.
(1)将![]() 代入
代入![]() ,得
,得![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() ,
,
得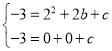 ,解得
,解得![]() .
.
所以抛物线![]() 对应的函数表达式为
对应的函数表达式为![]() .
.
(2)设点![]() 的坐标为
的坐标为![]() .
.
第一种情况:![]() 为平行四边形的一条边.
为平行四边形的一条边.
①当点![]() 在点
在点![]() 右侧时,则点
右侧时,则点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() ,得
,得
![]() ,
,
整理得![]() ,解得
,解得![]() .
.
因为![]() 时,点
时,点![]() 与点
与点![]() 重合,不符合题意,所以舍去,
重合,不符合题意,所以舍去,
此时点![]() 的坐标为
的坐标为![]() .
.
②当点![]() 在点
在点![]() 左侧时,则点
左侧时,则点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() ,得
,得
![]() ,
,
整理得![]() ,解得
,解得![]() .
.
此时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
第二种情况:当![]() 为平行四边形的一条对角线时.
为平行四边形的一条对角线时.
由![]() 的中点坐标为
的中点坐标为![]() ,得
,得![]() 的中点坐标为
的中点坐标为![]() ,
,
故点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() ,得
,得
![]() ,
,
整理得![]() ,解得
,解得![]() .
.
因为![]() 时,点
时,点![]() 与点
与点![]() 重合,不符合题意,所以舍去,
重合,不符合题意,所以舍去,
此时点![]() 的坐标为
的坐标为![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
(3)当点![]() 在
在![]() 轴左侧时,抛物线
轴左侧时,抛物线![]() 不存在动点
不存在动点![]() 使得
使得![]() 平分
平分![]() .
.
当点![]() 在
在![]() 轴右侧时,不妨设点
轴右侧时,不妨设点![]() 在
在![]() 的上方,点
的上方,点![]() 在
在![]() 的下方,
的下方,
过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则有
,则有![]() .
.
由![]() 平分
平分![]() ,得
,得![]() ,则
,则![]() ,
,
故![]() ,所以
,所以![]() .
.
设点![]() 坐标为
坐标为![]() ,
,
点![]() 坐标为
坐标为![]() ,
,
所以有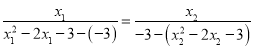 ,
,
整理得![]() .
.
在![]() 中,
中,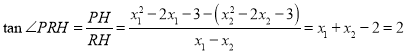 .
.
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .设点
.设点![]() 坐标为
坐标为![]() .
.
若![]() ,则需
,则需![]() .所以
.所以![]() .
.
所以![]() .解得
.解得![]() .
.
所以点![]() 坐标为
坐标为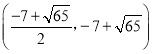 或
或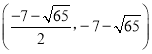 .
.


科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象交于A,B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C,设二次函数图象的顶点为D.
的图象交于A,B两点(点A在点B的左侧),与这个二次函数图象的对称轴交于点C,设二次函数图象的顶点为D.
(1)求点C的坐标;
(2)若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的解析式;
(3)若![]() ,且△ACD的面积等于10,请直接写出满足条件的点D的坐标.
,且△ACD的面积等于10,请直接写出满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
用![]() 的矩形瓷砖,可拼得一些长度不同但宽度均为
的矩形瓷砖,可拼得一些长度不同但宽度均为![]() 的矩形图案.
的矩形图案.
已知长度为![]() 的所有图案如下:
的所有图案如下:

(尝试操作)
在所给方格中(假设图中最小方格的边长为![]() ),尝试画出所有用
),尝试画出所有用![]() 的“矩形瓷砖”拼得的“长度是
的“矩形瓷砖”拼得的“长度是![]() ,但宽度均为
,但宽度均为![]() ”的矩形图案示意图.
”的矩形图案示意图.

(归纳发现)
观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.

(规律概括)
描述一下你发现的规律: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() 为圆弧上一点,
为圆弧上一点,![]() 垂直于过
垂直于过![]() 点的切线,垂足为
点的切线,垂足为![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
.![]() ,垂足为点
,垂足为点![]() .
.
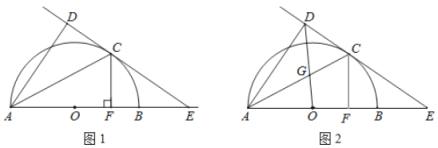
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() 时,求
时,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
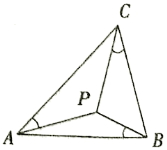
【题目】如图,若![]() 内一点
内一点![]() 满足
满足![]() ,则点
,则点![]() 为
为![]() 的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形
的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形![]() 中,
中,![]() .若
.若![]() 为
为![]() 的布洛卡点,
的布洛卡点,![]() ,则
,则![]() 的值为( )
的值为( )
A.10B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水产养殖户开发一个三角形状的养殖区域,A、B、C三点的位置如图所示.已知∠CAB=105°,∠B=45°,AB=100![]() 米.(参考数据:
米.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
≈1.73,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,结果保留整数)
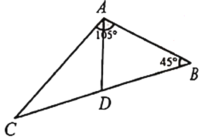
(1)求养殖区域△ABC的面积;
(2)养殖户计划在边BC上选一点D,修建垂钓栈道AD,测得∠CAD=40°,求垂钓栈道AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
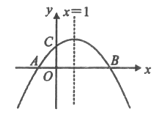
【题目】如图,已知二次函数![]() 的图象与x轴交于A,B两点,与y轴交于点C,
的图象与x轴交于A,B两点,与y轴交于点C,![]() ,对称轴为直线
,对称轴为直线![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的一个根,其中正确的有_________个
的一个根,其中正确的有_________个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生在新冠肺炎疫情影响期间在家进行体育锻炼的情况,王老师通过学生家长钉钉群对学生每天参加体育锻炼的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,根据图中信息,解答下列问题:
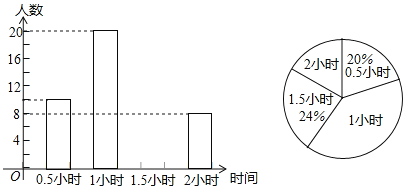
(1)填空:被调查的学生总数是______;每天体育锻炼时间为1.5小时的学生数是______;每天体育锻炼时间的中位数是______小时.
(2)补全条形统计图;
(3)该校共有1800名学生,请估计该校学生每天体育锻炼时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
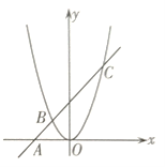
【题目】如图,在平面直角坐标系中,一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,与二次函数交于点
,与二次函数交于点![]() 、点
、点![]() ,点
,点![]() 三点的横坐标分别是
三点的横坐标分别是![]() ,则下面四个等式中不一定成立的是( )
,则下面四个等式中不一定成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com