
����Ŀ����ͼ��Rt��ABC�У���B=90 �� BC=12��tanC=![]() �� ���һ�ʵ�P��ʼʱ��AB�ߵ�P0����BP0=3��P��һ����P0����AC�ߵ�P1����1����㣩������
�� ���һ�ʵ�P��ʼʱ��AB�ߵ�P0����BP0=3��P��һ����P0����AC�ߵ�P1����1����㣩������![]() ���ڶ�����P1����BC�ߵ�P2����2����㣩������
���ڶ�����P1����BC�ߵ�P2����2����㣩������![]() ����������P2����AB�ߵ�P3����3����㣩������
����������P2����AB�ߵ�P3����3����㣩������![]() �������ʵ�P������������һֱ����ȥ����n�����ΪPn��nΪ�������������P2014���P2015֮��ľ���Ϊ�� ����
�������ʵ�P������������һֱ����ȥ����n�����ΪPn��nΪ�������������P2014���P2015֮��ľ���Ϊ�� ����
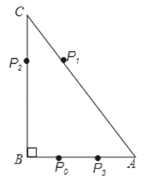
A. 6 B. 5 C. 4 D. 3
���𰸡�A
��������
�������⣬�۲�ѭ�����ɣ������ѣ������һ�㣬�ҵ���P2014�Լ���P2015��λ�ã������ó��𰸣�
��ͼ��ʾ��
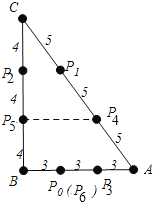
��Rt��ABC��
��BC=12��tan��C=![]() ����B=90�㣬
����B=90�㣬
��AB=9��AC=15��
�����⣺BP0=P0P3=P3A=3��AP4=P4P1=P1C=5��CP2=P2P5=P5B=4��
P6��P0�غϣ���P6��ʼ����ѭ����
��2014��6��������4��
��P2014��P4�غϣ�
��P2014P2015=P4P5��
��P4P5��BA��
��![]()
��![]()
��P4P5=6
��P2014P2015=P4P5=6��
��ѡ��A��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��1������֪������ABC�У���BAC��90����AB��AC��ֱ��l������A��BD��ֱ��l��CE��ֱ��l������ֱ�Ϊ��D��E��֤����DE��BD+CE��
��2����ͼ��2��������1���е�������Ϊ������ABC�У�AB��AC��D��A��E���㶼��ֱ��l�ϣ��ҡ�BDA����AEC����BAC������������Ϊ������ǻ�۽ǣ����ʽ���DE��BD+CE�Ƿ��������������������֤����������������˵�����ɣ�
��3����չ��Ӧ�ã���ͼ��3����D��E��ֱ��l�ϵ������㣨D��A��E���㻥���غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA����AEC����BAC����֤��DF��EF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
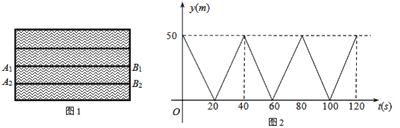
����Ŀ����ͼ1��A1B1��A2B2��ˮ�������ڵ�����������������������ƽ�е��߶Σ�������һ����Ӿ�˶�����������һ����Ӿ�����ߣ���������A1B1�ϴ�A1������������B1����ͬ�����ٶȷ���A1����Ȼ���ظ��������̣���������A2B2����2m/s���ٶȴ�B2������������A2������ͬ���ٶȻص�B2����Ȼ���ظ��������̣�������ÿ���۷�ʱ�ļ��ٺ�ת��ʱ�䣩�����ס�������ͬʱ���������뿪�ر�B1B2�ľ���Ϊy��m�����˶�ʱ��Ϊt��s�������ζ�ʱ��y��m����t��s���ĺ���ͼ����ͼ2��ʾ��
��1�������ij����� m�����ٶ��� m/s��
��2������������ʱ���ס������˵ڶ���������
��3�����Ӽס�������ͬʱ��ʼ������2����Ϊֹ���ס��ҹ������� �Σ�2����ʱ���Ҿ�ر�B1B2�ľ���Ϊ�����ס�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������и���ABC���DEF��
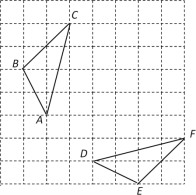
��1����ABC���DEF�Ƿ�ȫ�ȣ�����˵���ɣ���
��2����ABC���DEF�Ƿ����Գƣ�����˵���ɣ���
��3������ABC���DEF����Գƣ��뻭�����ĶԳ���l������ֱ��l�ϻ�����P��ʹPA+PC��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�E��AB���е㣬AD//EC����AED=��B��
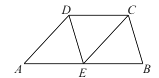
��1����֤����AED�ա�EBC��
��2����AB=6ʱ����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������a3��2+a6��_____��
��2��2a5b����ab��3��_____��
��3��![]() ��_____��
��_____��
��4������a��3����a��4��_____��
��5����x+2����x��3����_____��
��6����2��103������5��104����_____�����ÿ�ѧ��������ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC����ABD�Ľ�ƽ���ߣ�BC=DC����A=��E=30�㣬��D=50�㣮
��1��д��AB=DE�����ɣ�
��2������BCE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������E��ÿ��1����λ���ȵ��ٶȴӵ�A������AC�����˶�����Fͬʱ��ÿ��1����λ���ȵ��ٶȴӵ�C������CA�����˶�����AC��12��BD��8����________����ı���BEDF�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ�������֣�-1��1��2�Ŀ�Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ����������һ�ż������֣��Ż�ϴ�Ⱥ��ٴ���������һ�ż������֣�
(1)�����б�������ͼ�ķ�����ֻѡ����һ�֣�����ʾ���γ����Ƭ�ϵ����ֵ����н����
(2)����һ�γ����������Ϊ��ĺ�����x���ڶ��γ����������Ϊ���������y����㣨x��y������˫����![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com