
【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:

a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
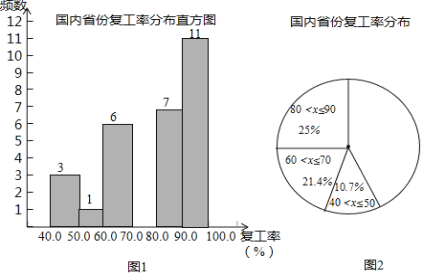
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.
【答案】(1)补全图形见解析;(2)12.9;(3)88.5;(4)全国28个省份中,复工率在90%以上的所占的比重大,达到40%.其次是复工率在80<x≤90区间的占25%,复工率小于50%以下的仅占10.7%,表明随着疫情的逐渐好转,全国各个省份各行各业经济逐步恢复正常.
【解析】
(1)根据题意补全频数分布直方图即可;
(2)根据题意用360°乘以50<x≤60这组所占比例,列式计算即可;
(3)由题意直接根据中位数的定义进行分析即可得到结论;
(4)根据题意简述国内企业截止3月1日的复工率分布特征即可.
解:(1)被调查的省份有7÷25%=28(个),
复工率在90<x≤100的省份有11个,
∴复工率在50<x≤60的省份有28﹣(3+6+7+11)=1(个),
补全频数分布直方图如图所示;
(2)扇形统计图中50<x≤60这组的圆心角度数是360°×![]() ≈12.9°;
≈12.9°;
故答案为:12.9;
(3)28个数据中按照从小到大排列中位数是第14和15个数的平均数,即![]() =88.5;
=88.5;
(4)通过统计表可以得到截止3月1号,全国28个省份中,复工率在90%以上的所占的比重大,达到40%.其次是复工率在80<x≤90区间的占25%,复工率小于50%以下的仅占10.7%,表明随着疫情的逐渐好转,全国各个省份各行各业经济逐步恢复正常.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
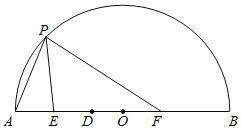
【题目】如图,D是直径AB上一定点,E,F分别是AD,BD的中点,P是![]() 上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
上一动点,连接PA,PE,PF.已知AB=6cm,设A,P两点间的距离为xcm,P,E两点间的距离为y1cm,P,F两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0.97 | 1.27 |
| 2.66 | 3.43 | 4.22 | 5.02 |
y2/cm | 3.97 | 3.93 | 3.80 | 3.58 | 3.25 | 2.76 | 2.02 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
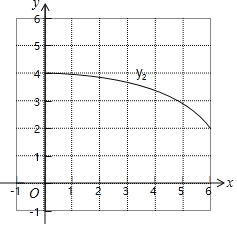
(3)结合函数图象,解决问题:当△PEF为等腰三角形时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物重量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为5kg(在弹性限度内)时,弹簧总长L(cm)是( )
A.22.5B.25C.27.5D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y=![]() (x>0)的图象G与直线l:y=2x﹣4交于点A(3,a).
(x>0)的图象G与直线l:y=2x﹣4交于点A(3,a).
(1)求k的值;
(2)已知点P(0,n)(n>0),过点P作平行于x轴的直线,与图象G交于点B,与直线l交于点C.横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当n=5时,直接写出区域W内的整点个数;
②若区域W内的整点恰好为3个,结合函数图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】明代的程大位创作了《算法统宗》,它是一本通俗实用的数学书,将枯燥的数学问题化成了美妙的诗歌,读来朗朗上口,是将数字入诗的代表作.其中有一首饮酒数学诗:“肆中饮客乱纷纷,薄酒名醨厚酒醇.醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮下19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点M为BC中点.点P为AB边上一动点,点D为BC边上一动点,连接DP,以点P为旋转中心,将线段PD逆时针旋转90°,得到线段PE,连接EC.
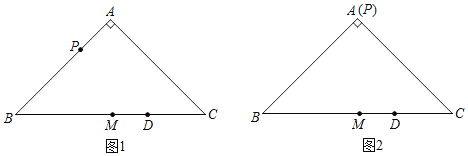
(1)当点P与点A重合时,如图2.
①根据题意在图2中完成作图;
②判断EC与BC的位置关系并证明.
(2)连接EM,写出一个BP的值,使得对于任意的点D总有EM=EC,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
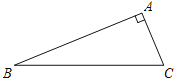
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
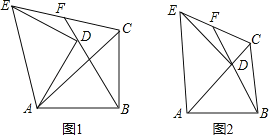
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F.
(1)如图2,当α=45°时,求证:CF=EF;
(2)在旋转过程中,①问(1)中的结论是否仍然成立?证明你的结论;②连接CD,当△CDF为等腰直角三角形时,求tan![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com