
分析 根据条件作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行求解即可.
解答 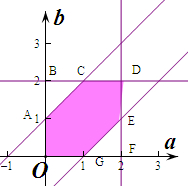 解:∵a,b∈[0,2],
解:∵a,b∈[0,2],
∴$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\end{array}\right.$,
则甲乙心有灵犀满足的条件为$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\\{|a-b|≤1}\end{array}\right.$,
作出不等式组对应的平面区域如图:
则G(1,0),F(2,0),E(2,1),
则三角形GFE的面积S=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
则正方形OBDF的面积S=2×2=4,
则阴影部分的面积S=4-2×$\frac{1}{2}$=4-1=3,
则他们“心有灵犀”的概率P=$\frac{3}{4}$.
点评 本题主要考查概率的计算,根据几何概型的概率公式,结合线性规划求出对应区域的面积是解决本题的关键.


科目:初中数学 来源: 题型:填空题
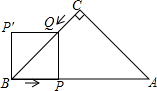 如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒$\sqrt{2}$cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPBP′为正方形,则t的值为2.
如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒$\sqrt{2}$cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPBP′为正方形,则t的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
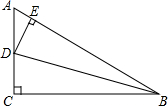 如图,在Rt△ABC中,BD平分∠ABC交AC于D,DE⊥AB,∠ABC=30°,若AB=3cm,则AD+DE=$\frac{3}{2}$cm.
如图,在Rt△ABC中,BD平分∠ABC交AC于D,DE⊥AB,∠ABC=30°,若AB=3cm,则AD+DE=$\frac{3}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
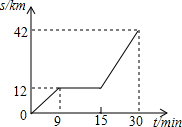 如图是某汽车行驶的路S(km)与时间t(min)的函数关系图,观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路S(km)与时间t(min)的函数关系图,观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
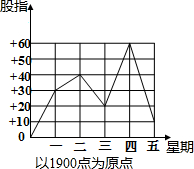 如图为某周上海股市的股指变化折线统计图:
如图为某周上海股市的股指变化折线统计图:| 星期 | 一 | 二 | 三 | 四 | 五 |
| 股指变化(点) | +30 | +10 | -20 | +40 | -50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将长方形ABCD沿对角线BD折叠后,点C落在C′处,BC′交AD于E,若AD=8,AB=6,则DE=$\frac{25}{4}$.
如图,将长方形ABCD沿对角线BD折叠后,点C落在C′处,BC′交AD于E,若AD=8,AB=6,则DE=$\frac{25}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com