
 如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$). 分析 先利用两点间的距离公式计算出AD=2,再根据菱形的性质得到CD=AD=2,CD∥AB,然后根据平行于x轴的直线上的坐标特征写出C点坐标.
解答 解:∵点D的坐标为(1,$\sqrt{3}$),
∴AD=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵四边形ABCD为菱形,
∴CD=AD=2,CD∥AB,
∴C点坐标为(3,$\sqrt{3}$).
故答案为(3,$\sqrt{3}$).
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了坐标与图形性质.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
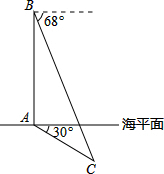 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7)
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
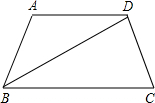 如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.
如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答:
已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2=(a+c)(a-c) | B. | a:b:c=1:2:$\sqrt{3}$ | C. | a=32,b=42,c=52 | D. | a=6,b=8,c=10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com