
【题目】如图①,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来 ;
(2)求证:BG=DG,AG=CG;
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
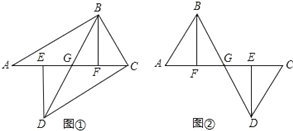
【答案】(1)3对,△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD;(2)证明见解析;(3)成立,证明见解析.
【解析】
试题(1)利用A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD可判断全等三角形的个数.
(2)先根据DE⊥AC,BF⊥AC,AE=CF,求证△ABF≌△CDE,再求证△DEG≌△BFG,即可.
(3)先根据DE⊥AC,BF⊥AC,AE=CF,求证△ABF≌△CED,再求证△BFG≌△DEG,即可得出结论.
试题解析:(1)图①中有3对全等三角形,它们是△AFB≌△DEC,△DEG≌△BFG,△AGB≌△CGD.
理由:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
∴△DEG≌△BFG,
∴EG=FG,DG=BG,
∵∠AGB=∠CGD,
∴△AGB≌△CGD;
(2)∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴ED=BF.
由∠AFB=∠CED=90°得DE∥BF,
∴∠EDG=∠GBF,
∵∠EGD和∠FGB是对顶角,ED=BF,
∴△DEG≌△BFG,
∴EG=FG,DG=BG,
(3)第(2)题中的结论成立,
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE,
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
在Rt△ABF和Rt△CDE中,
![]()
∴Rt△ABF≌Rt△CED(HL),
∴BF=ED.
∵∠BFG=∠DEG=90°,
∴BF∥ED,
∴∠FBG=∠EDG,
∴△BFG≌△DEG,
∴FG=GE,BG=GD,
即第(2)题中的结论仍然成立.


科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要测量一幢楼CD的高度,在地面上A点测得楼CD的顶部C的仰角为30°,向楼前进50m到达B点,又测得点C的仰角为60°. 求这幢楼CD的高度(结果保留根号).
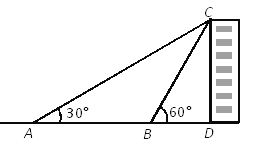
【答案】该幢楼CD的高度为25![]() m .
m .
【解析】试题分析:根据题意得出![]() 的度数,进而求出
的度数,进而求出![]() ,进而利用
,进而利用![]() 求出即可.
求出即可.
试题解析:依题意,有![]()
∵![]()
∴![]()
∴![]()
在![]() 中,
中, ![]() (m),
(m),
∴ 该幢楼CD的高度为25![]() m .
m .
【题型】解答题
【结束】
23
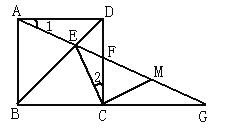
【题目】如图,正方形ABCD中,E是BD上一点,AE的延长线交CD于F,交BC的延长线于G,M是FG的中点.
(1)求证:① ∠1=∠2;② EC⊥MC.
(2)试问当∠1等于多少度时,△ECG为等腰三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
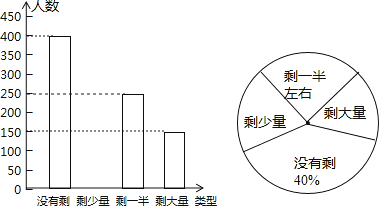
(1)这次被调查的同学共有 名;“剩大量”的扇形圆心角是 .
(2)把条形统计图补充完整;
(3)在被调查的学生中随机抽取一名恰巧是“剩少量”或“剩一半左右”饭的概率多大;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数![]() 的图象经过点(3,-6).
的图象经过点(3,-6).
(1)求这个函数的表达式;
(2)在如图所示的直角坐标系中画出这个函数的图象;
(3)判断点A(4,-2)、B(-1.5,3)是否在这个函数的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子摆成如图所示的“T”字图案.

(1)摆成第一个“T”字需要多少枚棋子,第二个呢?按这样的规律摆下去,摆成第10个“T”字需要多少枚个棋子?
(2)第![]() 个需多少枚棋子?
个需多少枚棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两个木工组,甲组每天修理桌椅16套,乙组每天修理桌椅比甲组多8套.甲组单独修理完这些桌椅比乙组单独修理完多用20天.学校每天付甲组80元修理费,付乙组120元修理费.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天20元生活补助费.现有三种修理方案:
方案一,由甲组单独修理;
方案二,由乙组单独修理;
方案三,甲、乙两组同时修理.
你认为哪种方案省时又省钱?为什么.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com