Question

有一批长50米的钢筋，现要截成长度为9.5米和7米的两种钢筋备用，问怎样截法可使原材料的利用率最高？并求利用率是多少？

Answer 1

解：设截成长度为9.5米的有x段，截成7米的有y段，还剩z米．
则由题意得 z=50-9.5x-7y
又∵x≥1、y≥1、z≥0．
∴50-9.5x-7y≥0?7y≤50-9.5x?7≤7y≤50-9.5x
∴1≤x≤4
①当x=1时，则z=40.5-7y
y最大取5，此时z=5.5；
②当x=2时，则z=31-7y
y最大取4，此时z=3；
③当x=3时，则z=21.5-7y
y最大取3，此时z=0.5；
④当x=4时，此时z=12-7y
y最大取1，此时z=5．
所以要使原材料的利用率最高截成长度为9.5米的有3段，截成7米的有3段，还剩0.5米；那么利用率=．
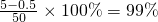
答：当截成长度为9.5米的有3段，截成7米的有3段时，可使原材料的利用率最高为99%．
分析：首先假设截成长度为9.5米的有x段，截成7米的有y段，还剩z米．
根据题意列出方程z=50-9.5x-7y，找到隐含条件x≥1、y≥1、z≥0．进一步根据该方程及隐含条件确定x的具体取值范围为1≤x≤4．再分别当x=1、2、3、4时，讨论y、z的取值，寻找到符合条件的取值．
点评：本例是最简单的下料问题，属于“线性规划”的范畴，线性规划是运用一次方程（组）、一次函数来解决规划问题的数学分支．规划论研究的问题主要有两类：一确定了一项任务，研究怎样精打细算使用最少人力、物力和时间去完成它；另一类是在已有一定数量的人力、物力和财力的条件下，研究怎样合理调配，使它们发挥最大限度的作用，从而完成最多的任务．
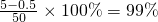