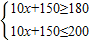云南省公路建设发展速度越来越快,通车总里程已位居全国第一,公路的建设促进了广大城乡客运的发展.某市扩建了市县级公路,某运输公司根据实际需要计划购买大,中型客车共10辆,大型客车每辆价格为25万元,中型客车每辆价格为15万元.
(1)设购买大型客车x(辆),购车总费用为y(万元),求y与x之间的关系式;
(2)若购车资金为180万元至200万元(含180万元和200万元),那么有几种购车方案在确保交通安全的前提下,根据客流量调查,大型客车不能少于4辆,此时如何确定购车方案可使该运输公司购车费用最少?
【答案】
分析:(1)依题意可得y与x的关系式为y=25x+15(10-x);
(2)根据(1)的答案可有三种购车方案.购车总费用=25×大型客车数量+15×中型客车的数量.
解答:解:(1)由题意得y=25x+15(10-x)
即y=10x+150.
(2)由题意得
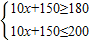
解得3≤x≤5
因为x是正整数
故x可取3,4,5三个值,所以有三种购车方案:
①购大型客车3辆,中型客车10-3=7(辆);
②购大型客车4辆,中型客车10-4=6(辆);
③购大型客车5辆,中型客车10-5=5(辆).
又大型客车不少于4辆,故可得x=4或x=5.
当x=4时,y=25×4+15×(10-4)=190(万元);
当x=5时,y=25×5+15×(10-5)=200(万元).
因为190<200,
所以购大型客车4辆,中型客车6辆可满足要求,且购车费用最少.
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.