
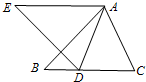
 如图,△ABC按顺时针方向转动一个角后成为△AED,且点D恰好在边BC上,若∠EAB=40°,则∠C=
如图,△ABC按顺时针方向转动一个角后成为△AED,且点D恰好在边BC上,若∠EAB=40°,则∠C= 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠B=30°,将△ABC绕着点A按顺时,针方向旋转到△AB′C′,使B′落在CA的延长线上,则△ABC的旋转度数是
如图,在Rt△ABC中,∠B=30°,将△ABC绕着点A按顺时,针方向旋转到△AB′C′,使B′落在CA的延长线上,则△ABC的旋转度数是查看答案和解析>>
科目:初中数学 来源:2012届河南省虞城县营盘中学中考模拟三数学卷(带解析) 题型:解答题
Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△ 位置,直线
位置,直线 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南省中考模拟三数学卷(解析版) 题型:解答题
Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△ 位置,直线
位置,直线 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com