
【题目】学习概念:
三角形一边的延长线与三角形另一边的夹角叫做三角形的外角.如图1中∠ACD是△AOC的外角,那么∠ACD与∠A、∠O之间有什么关系呢?
∵∠ACD=180°﹣∠ACO,∠A+∠O=180°﹣∠ACO
∴∠ACD=∠A+ ,
结论:三角形的外角等于与它不相邻的两个内角的 .
问题探究:
(1)如图2,已知:∠AOB=∠ACP=∠BDP=60°,且AO=BO,则△AOC △OBD;
(2)如图3,已知∠ACP=∠BDP=45°,且AO=BO,当∠AOB= °,△AOC≌△OBD;
应用结论:

(3)如图4,∠AOB=90°,OA=OB,AC⊥OP,BD⊥OP,请说明:AC=CD+BD.
拓展应用:
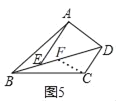
(4)如图5,四边形ABCD,AB=BC,BD平分∠ADC,AE∥CD,∠ABC+∠AEB=180°,EB=5,求CD的长.
【答案】∠O,和;(1)≌;(2)45°;(3)见解析;(4)CD=5.
【解析】
学习概念:∠ACD=∠A+∠O,理由是等量代换,所以得到结论:三角形的外角等于与它不相邻的两个内角的和.问题探究:(1)由邻补角互补可知∠ACO=∠ODB=120°,由外角性质可知∠AOC+∠OAC=∠ACP=60°,等量代换得∠OAC=∠BOD,进而可证三角形△AOC和△OBD全等.(2)当∠AOB=45°时,△AOC≌△OBD,证法同(1).(3)先证明△AOC≌△OBD,可得OC=BD,AC=OD,进而可证AC=CD+BD.
(4)在DB上取一点F使CF=CD,由BD平分∠ADC,AE∥CD,可得∠AED=∠CFD,再利用等量代换,可得∠BAE=∠CBF,然后可证△ABE≌△BCF,进而可得CD=BE=5.
解:
学习概念:
∵∠ACD=180°﹣∠ACO,∠A+∠O=180°﹣∠ACO
∴∠ACD=180°﹣(180°﹣∠A﹣∠O)=∠A+∠O,
即:三角形的外角等于与它不相邻的两个内角的和,
故答案为:∠O,和.
问题探究:(1)∵∠ACP=∠BDP=60°,
∴∠ACO=∠ODB=120°,∠AOC+∠OAC=∠ACP=60°,
∵∠AOB=∠AOC+∠BOD=60°,
∴∠OAC=∠BOD,
在△AOC和△OBD中,
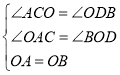 ,
,
∴△AOC≌△OBD(AAS),
故答案为:≌.
(2)当∠AOB=45°时,△AOC≌△OBD,理由如下,
同(1)∵∠ACP=∠BDP=45°,
∴∠ACO=∠ODB=135°,∠AOC+∠OAC=∠ACP=45°,
∵∠AOB=∠AOC+∠BOD=45°,
∴∠OAC=∠BOD,
在△AOC和△OBD中,
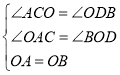 ,
,
∴△AOC≌△OBD(AAS),
故当∠AOB=45°时,△AOC≌△OBD.
(3)∵AC⊥OP,BD⊥OP,
∴∠ACO=∠ODB=90°,
∴∠1+∠3=90°,
∵∠AOB=90°,
∴∠2+∠3=90°,
∴∠1=∠2,
∴△AOC≌△OBD,
∴OC=BD,AC=OD,
∴AC=OD=OC+CD=BD+CD,
(4)如图5,在DB上取一点F使CF=CD,
∴∠CFD=∠CDF,
∵BD平分∠ADC,
∴∠ADB=∠CDB,
∴∠CFD=∠CDF=∠ADB,
∵AE∥CD,
∴∠BDC=∠AED,
∴∠AED=∠CFD,
∵∠AEB+∠AFD=180°,∠AEB+∠ABC=180°,
∴∠AED=∠ABC,
∴∠AEB=∠BFC,
∵∠AED=∠ABE+∠BAE,∠ABC=∠ABE+∠CBF,
∴∠BAE=∠CBF,
∵AB=BC,
∴△ABE≌△BCF,
∴CF=BE,
∴CD=CF=BE =5.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AC=5,AB=12,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AC的延长线于点E,DF⊥AB于点F.

(1)求证:CE=BF;
(2)求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() .
.
(1)当m=2时,请解关于x、y的方程组![]() ;
;
(2)若关于x、y的方程组![]() 中,x为非负数、y为负数,
中,x为非负数、y为负数,
①试求m的取值范围;
②当m取何整数时,不等式3mx+2x>3m+2的解为x<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com