
 如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系?
如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系? 分析 结论:S△ABC=9•S△A′B′C′.只要证明$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$=$\frac{1}{3}$,推出△ABC∽△A′B′C′,推出$\frac{{S}_{△A′B′C′}}{{S}_{△ABC}}$=($\frac{1}{3}$)2=$\frac{1}{9}$,即可证明.
解答 解:S△ABC=9•S△A′B′C′.
理由: ∵A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,
∵A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,
∴$\frac{A′B′}{AB}$=$\frac{OA′}{OA}$=$\frac{OB′}{OB}$=$\frac{1}{3}$,$\frac{B′C′}{BC}$=$\frac{OB′}{OB}$,$\frac{A′C′}{AC}$=$\frac{OA′}{OA}$,
∴$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$=$\frac{1}{3}$,
∴△ABC∽△A′B′C′,
∴$\frac{{S}_{△A′B′C′}}{{S}_{△ABC}}$=($\frac{1}{3}$)2=$\frac{1}{9}$,
∴S△ABC=9•S△A′B′C′.
点评 本题考查相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
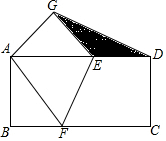 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )| A. | 5 | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
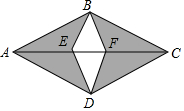 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
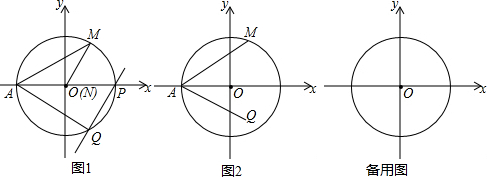
 如图,在平面直角坐标系中.O为坐标原点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A,B两点.点P从点A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.过点P与直线AB垂直的直线与y轴交于点E.
如图,在平面直角坐标系中.O为坐标原点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A,B两点.点P从点A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.过点P与直线AB垂直的直线与y轴交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com