
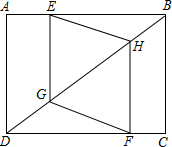
 如图,矩形ABCD中,BC=3,AB=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE=$\frac{7}{8}$.
如图,矩形ABCD中,BC=3,AB=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE=$\frac{7}{8}$. 分析 首先连接EF交BD于O,由矩形ABCD中,四边形EGFH是菱形,易证得△CDOF≌△BOE(AAS),即可得OB=OD,然后由勾股定理求得BD的长,继而求得OD的长,又由△DOF∽△DCB,利用相似三角形的对应边成比例,即可求得答案.
解答 解:连接EF交BD于O,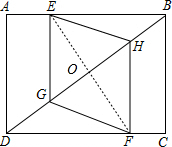
∵四边形EGFH是菱形,
∴EF⊥BD,OE=OF,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB∥CD,AB=DC=4,
∴∠ABO=∠FDO,
在△OEB与△OFD中,
$\left\{\begin{array}{l}{∠EBO=∠FDO}\\{∠EOB=∠FOD}\\{OE=OF}\end{array}\right.$,
∴△OEB≌△OFD(AAS),
∴BO=DO,
∵AC=$\sqrt{B{C}^{2}+D{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BO=$\frac{1}{2}$AC=$\frac{5}{2}$,
∵∠ODF=∠BDC,∠DOF=∠C=90°,
∴△DOF∽△DCB,
∴$\frac{DO}{DC}$=$\frac{DF}{BD}$,
∴$\frac{\frac{5}{2}}{4}$=$\frac{DF}{5}$,
∴DF=$\frac{25}{8}$,
∴BE=DF=$\frac{25}{8}$,
∴AE=AB-BE=4-$\frac{25}{8}$=$\frac{7}{8}$,
故答案为:$\frac{7}{8}$.
点评 此题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
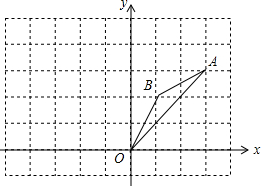 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,3),B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,3),B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=$\frac{1}{3}$ | B. | 3(x-1)2=$\frac{1}{3}$ | C. | (3x-1)2=1 | D. | (x-1)2=$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚均匀的六面体骰子,骰子停止后朝上的点数是6 | |
| B. | 打开电视机,任意选择一个频道,正在播新闻 | |
| C. | 在地球上,抛出去的篮球会下落 | |
| D. | 随机地从0,1,2,…,9这十个数中选取两个数,和为20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com