
如图所示,在四边形ABCD中,∠ADC=∠ABC=![]() ,AD=CD,DP⊥AB于P,若四边形ABCD的面积是18,求DP的长.
,AD=CD,DP⊥AB于P,若四边形ABCD的面积是18,求DP的长.
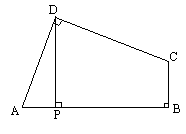
|
解:粗看此题,确实尤其困难,但只要细心观察到AD=DC,∠ADC= 将△DAP绕点D以逆时针方向旋转 因为∠ADC=∠ABC= 故∠A+∠DCB= 又∠A=∠DC 所以 又∠ 所以四边形DPB 又因为DP=D 所以四边形DPB
又△APD≌△DC 而S四边形ABCD=18=S正方形DPB 所以DP= |


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com