
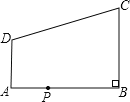
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】
试题分析:由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.
解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC,
∴∠A=180°﹣∠B=90°,
∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得x=![]() ;
;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得x=2或x=6.
∴满足条件的点P的个数是3个,
故选:C.


科目:初中数学 来源: 题型:
【题目】已知:线段AB=20cm.
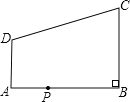
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(2)如图2:AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是﹣1,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3![]() .分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
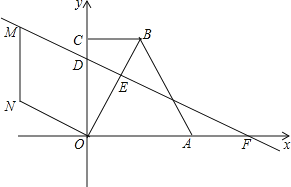
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;
(3)点M在(2)中直线DE上,四边形ODMN是菱形,求N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
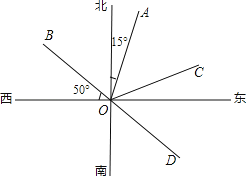
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
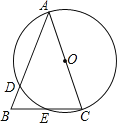
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D、E分别在AC、BC边上,且∠DOE=90°,DE交OC于P,下列结论:
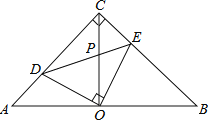
①图中的全等三角形共有3对;
②AD=CE;
③∠CDO=∠BEO;
④OC=DC+CE;
⑤△ABC的面积是四边形DOEC面积的2倍.
正确的是 .(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com